内部摩擦角は既にこれまでのブログ内で使われているワードですが、改めてこれについて解説いたします。
内部摩擦角ϕとは、土粒子同士の摩擦やかみ合わせによって生じるせん断抵抗を角度で表したものです。これは、土が外力によってせん断されるときに、どれだけ抵抗するかを示す重要な力学的パラメータです。
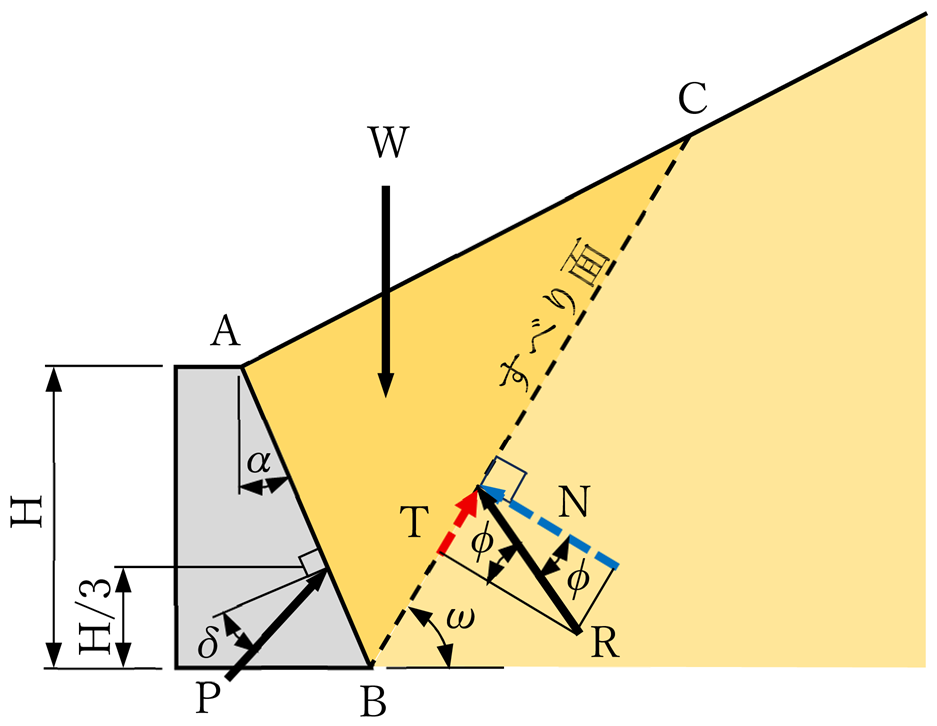
下図に示す、すべり土塊の重量Wに対するすべり面での反力Rはすべり面に対して直角（青矢印N）ではなく、少し下側の方から支えるような方向（角度）で反力（黒矢印R）が発生すると考えます。ここは感覚で理解できると思いますが、その角度が内部摩擦角ϕです。そして反力Rが角度ϕで斜めになったことによる、すべり面上で生じる抵抗力（赤色矢印）がせん断抵抗として生じることになります。
角度ではなく、摩擦係数 μ を使っても理論的には同じ情報を表現できます。しかし、角度 φ の方が視覚的・幾何学的に扱いやすいため、土質力学では角度で表現するのが一般的です。
それを示すのが「モール・クーロン破壊基準」との親和性です。モール・クーロン破壊基準では、応力状態をモール円と破壊包絡線で図示します。この破壊包絡線の傾きが ϕ（内部摩擦角）であり、角度で表すことで図的に理解しやすくなります。
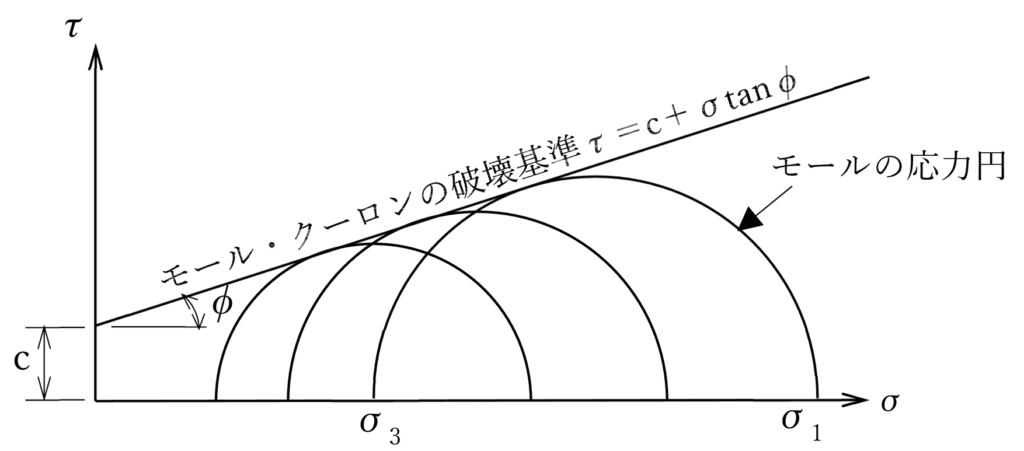
下図は応力状態の異なる3種の三軸圧縮試験での側圧σ3を加えた状態で破壊したときの垂直応力σ1の破壊包絡線がτ＝c+σtanφで表されていますが、ϕはちょうど包絡線の傾きを表すのに角度表現とすると分かりやすいという利点があります。
※τ＝c+σtanφは一般論であり、擁壁では擁壁背面が埋め戻しによる裏込め土なので締固めを行いやすい砂質土を用いるので、粘着力cの効果は考慮せずτ＝σtanφです。
以上で内部摩擦角について説明を行いましたが、ついでに内部摩擦角についての歴史にも触れたいと思います。
17～18世紀フランスの初期土圧理論では、土砂が自然に堆積したときの自由表面の最大傾斜角として「安息角」が利用されました。「自然傾斜角（natural slope）」とも呼ばれ、その角度以上になると土粒子は滑り落ち、角度は安定値に戻ります。
そして、この「安息角」がすべり面の角度でもあり、内部摩擦角ϕとしても利用されていました。上の写真にあるゆるい砂山の表面角度です。
Charles-Augustin de Coulomb（1776年）と後の Christian Otto Mohr によって、土の破壊条件が「粘着力 + 摩擦力」によって決まるという理論が提唱されました。
この理論では、内部摩擦角 ϕは応力状態に依存する力学的パラメータとして定義され、単なる斜面角度や安息角とは異なることが明確になりました。上の図がそれを示しています。
乾燥砂などの粗粒土に対して、安息角を測定することで内部摩擦角を推定する試みが行われましたが、以下のような関係が導かれました。
tanβ ≤ tanϕ ⇒ β ≤ ϕ
ここで β は安息角、ϕ は内部摩擦角。
極限状態（安全率1.0）では ϕ ≈ β となるが、一般には ϕ > β。
つまり、安息角は内部摩擦角の下限的指標に過ぎず、力学的には異なる概念です。
17～18世紀に安息角が内部摩擦角として扱われていた頃は、ドイツでは土質ごとに標準的な安息角を定めていたようです。
現在では、ボーリング孔内で行う標準貫入試験によるN値から推定式で求めることができます。推定式はϕ = 4.8logN1 + 21です。当ブログの「技術計算」内にある「せん断抵抗角の計算」でも紹介しています。昔（平成の半ばくらい）まではϕ=15＋√(15N)がかなり使われていましたが、現在はそれを用いることはほぼなくなっています。理由は、昔の式は過度に安全側であり小さいϕを算出するためです。
また、室内試験では「一面せん断試験」「一軸圧縮試験」「三軸圧縮試験」を行うことで求められます。乱さない砂のサンプリングは非常に難しく、主に軟弱地盤での粘性土の粘着力を求める場合が多いですが、粘性土でも内部摩擦角を期待することで対策規模を抑える効果が大きい大規模な構造物の設計では「三軸圧縮試験」で内部摩擦角を求めることがあります。
