クーロン土圧について解説

　前回は土圧係数について概説しましたが、今回は土圧係数を求めるための方法として現在ランキンと共に最も有名なクーロンの土圧論について解説したいと思います。

目次閉じる

クーロン土圧論
- 前提条件
- クーロン土圧論
クーロン土圧による最大土圧の導出
適用される構造物
まとめ

クーロン土圧論

前提条件

　クーロン土圧の前提条件は以下になります。

　　①粘着力ｃ＝0

　　②内部摩擦角 φ ≠ 0°

　　③壁面摩擦角 δ ≠ 0°

　　④壁面傾斜 α ≥ 0°

　　⑤地表面傾斜 β ≥ 0°

　　⑥すべり面　最大土圧の角度 ω ≈ 55°

　　⑦解析方法　滑動くさびのつり合い

　　⑧破壊基準　τ＝σtanφ

　　⑨土圧係数 K_A 　　φ、δ、α、βに依存

　　⑩土圧の作用方向壁法線からδ°

　　⑪上載荷重 q = 0

クーロン土圧論

　クーロン土圧について、下図のようなケースを想定してみます。擁壁形状は背面側はαの傾斜があり、背面土の勾配もβの傾斜があります。土圧の作用形態は主動土圧です。

図ー１　主動状態の壁と土の挙動

図ー２　土圧の作用

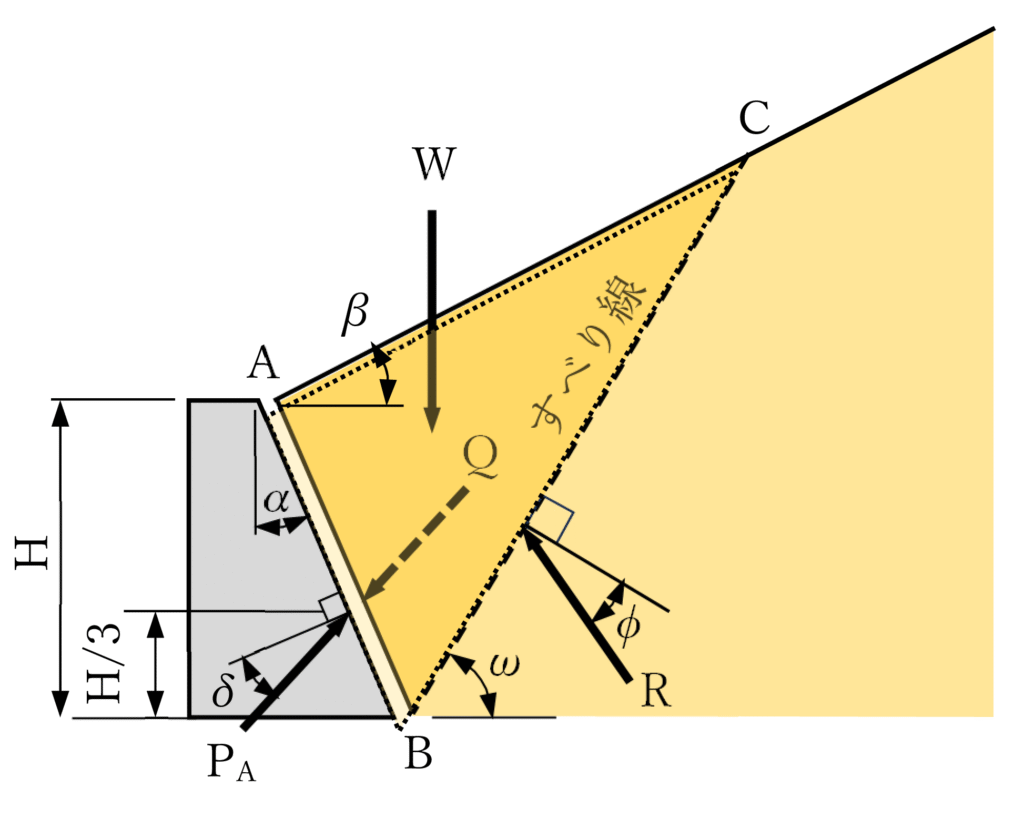
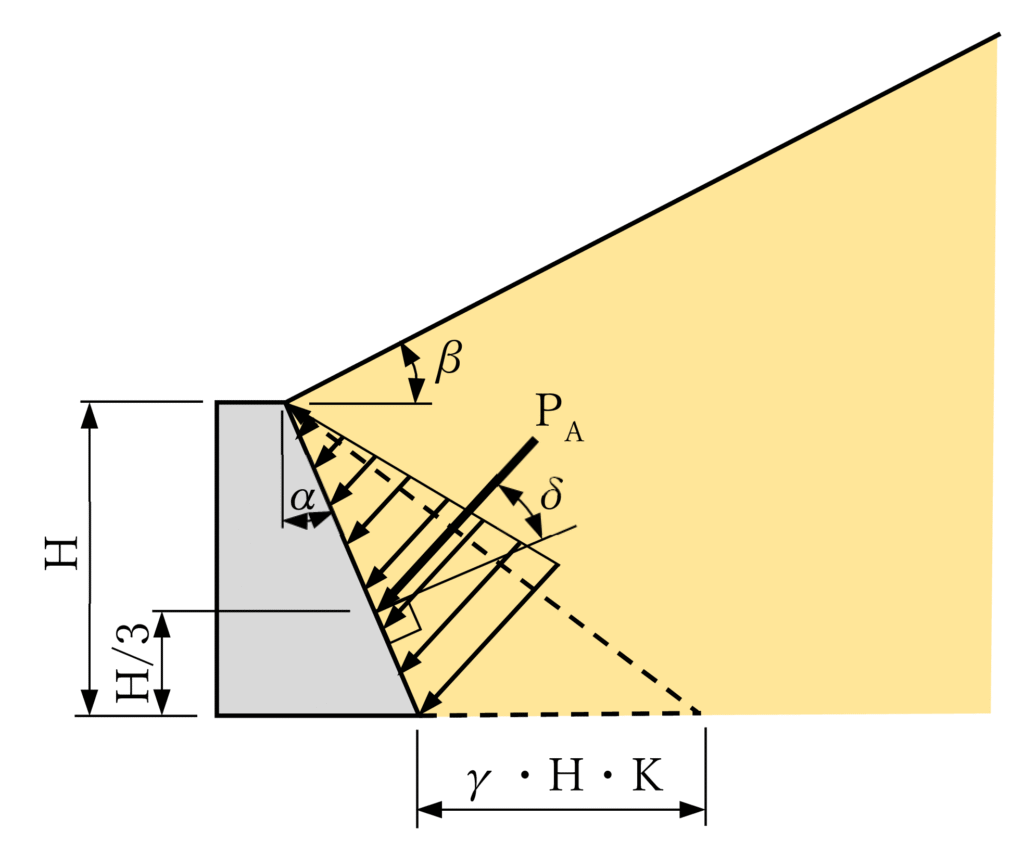
　いま、図ー１のように壁体が背面土から離れる方向（主動状態）にわずかに変位すると、背面土にすべり面が生じ、△ABCの土塊が壁体とすべり面に沿って下方に移動しようとします。この土塊は、壁面（AB）、地表面（AC）、滑り面（BC）で囲まれた三角形とします。壁背面は鉛直面と角度αをなし、滑り面は水平面と角度ωをなすとします。そのとき、土塊に働く力を図ー３のように考えます。土塊の重量W、滑り面（BC）に働く反力R（内部摩擦角φによるせん断抵抗を考慮）、壁面（AB）に作用する土圧の合力P（壁面摩擦角δによる摩擦抵抗を考慮）です。重量Wは土塊の自重（γ⋅面積△ABC）、Rは滑り面に垂直でφの摩擦力、Pは壁面に対しδ傾いた方向に作用するとします。力の釣り合い（水平・鉛直方向の力の総和＝0）を、壁背面角度α、地表面傾斜β、滑り面角度ω、内部摩擦角φ、壁面摩擦角δを用いて式で表します。土圧（P）はωの関数となり、Pが最大となるωをを求めるため、Pをωで微分（dP/dω=0）し、最大土圧P_Aを決定します。このプロセスを基に主動土圧係数K_Aを導出し、図ー２のように合力P_A=1/2γH²K_Aを計算する理論がクーロン土圧理論とされます。

図ー３　力のつりあい

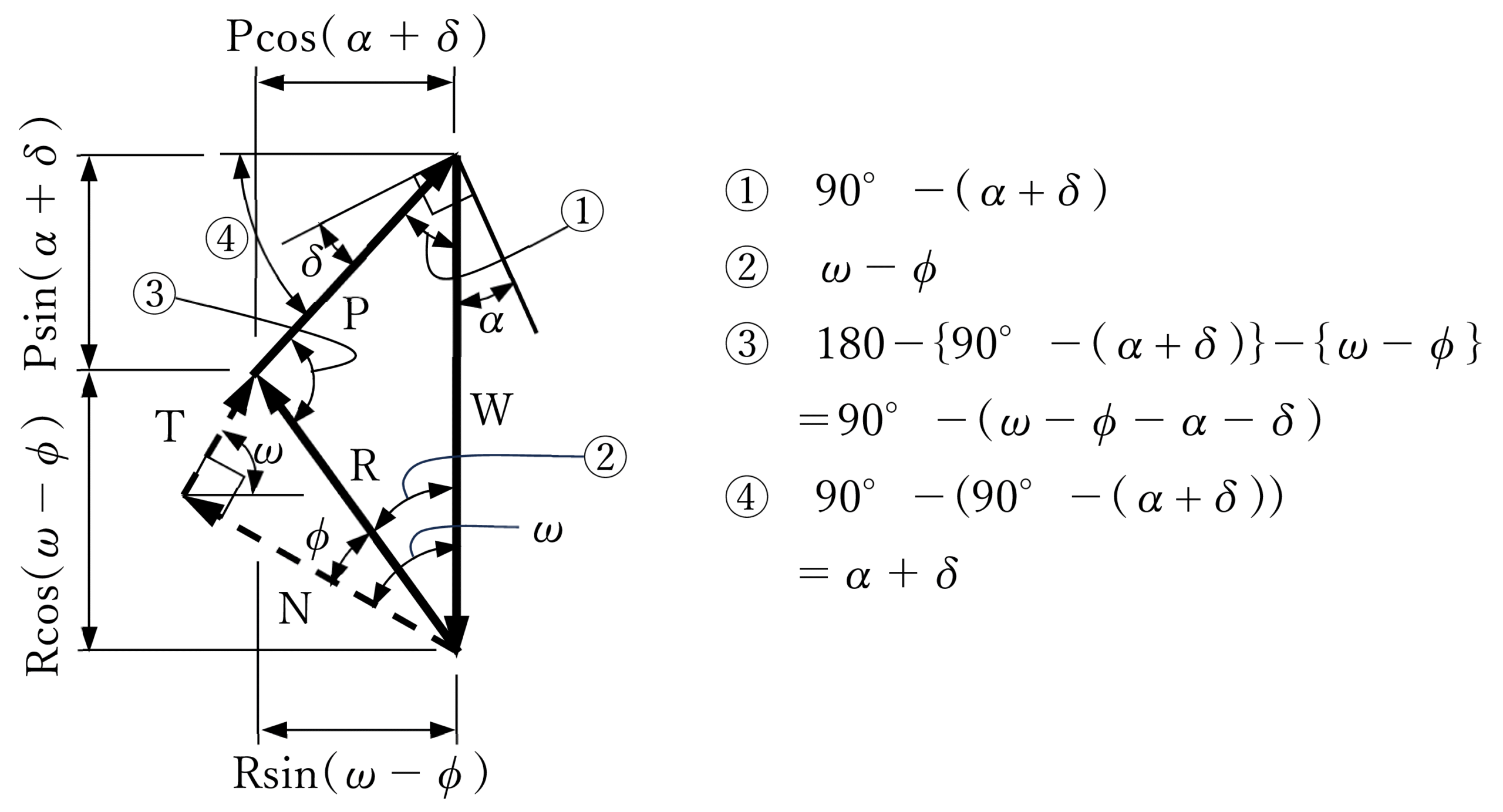
クーロン土圧による最大土圧の導出

滑動くさび△ABCの面積と力のつり合いから \( K_A \) までの導出

1. 面積式

\[ \triangle ABC = \left( \frac{H}{\cos \alpha} \right)^2 \cdot \frac{\sin(90^\circ – \alpha + \beta) \cdot \sin(90^\circ – \omega + \alpha)}{2 \cdot \sin(180^\circ – \omega + \beta)} \]

三角関数を整理： \[ \sin(90^\circ – \alpha + \beta) = \cos(\alpha – \beta), \quad \sin(90^\circ – \omega + \alpha) = \cos(\omega – \alpha) \] \[ \sin(180^\circ – \omega + \beta) = \sin(\omega – \beta) \] \[ \triangle ABC = \frac{H^2}{2 \cos^2 \alpha} \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha)}{\sin(\omega – \beta)} \]
重量： \[ W = \gamma \cdot \triangle ABC = \gamma \cdot \frac{H^2}{2 \cos^2 \alpha} \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha)}{\sin(\omega – \beta)} \]

2. 力のつり合い

水平方向： \[ P \cos(\alpha + \delta) – R \sin(\omega – \phi) = 0 \] \[ R = \frac{P \cos(\alpha + \delta)}{\sin(\omega – \phi)} \]
鉛直方向： \[ -W + P \sin(\alpha + \delta) + R \cos(\omega – \phi) = 0 \]
代入： \[ -W + P \sin(\alpha + \delta) + \left( \frac{P \cos(\alpha + \delta)}{\sin(\omega – \phi)} \right) \cos(\omega – \phi) = 0 \] \[ P \left[ \sin(\alpha + \delta) + \frac{\cos(\alpha + \delta) \cos(\omega – \phi)}{\sin(\omega – \phi)} \right] = W \] \[ \sin(\alpha + \delta) \sin(\omega – \phi) + \cos(\alpha + \delta) \cos(\omega – \phi) = \cos((\alpha + \delta) – (\omega – \phi)) = \cos(\omega – \phi – \alpha – \delta) \]
指針（道路土工擁壁工指針）の形式： \[ P \cdot \frac{\cos(\omega – \phi – \alpha – \delta)}{\sin(\omega – \phi)} = W \] \[ P = W \cdot \frac{\sin(\omega – \phi)}{\cos(\omega – \phi – \alpha – \delta)} \]

3. \( P \) の式に \( W \) を代入

\( W \)： \[ W = \gamma \cdot \frac{H^2}{2 \cos^2 \alpha} \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha)}{\sin(\omega – \beta)} \]
代入： \[ P = \left( \gamma \cdot \frac{H^2}{2 \cos^2 \alpha} \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha)}{\sin(\omega – \beta)} \right) \cdot \frac{\sin(\omega – \phi)}{\cos(\omega – \phi – \alpha – \delta)} \] \[ = \frac{1}{2} \gamma H^2 \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \]

4. \(\omega\) の最適化（最大土圧）

\( P \) を最大化するため、\( \omega \) で微分： \[ P = \frac{1}{2} \gamma H^2 \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \]
微分 \(\frac{dP}{d\omega} = 0\) を解く（詳細は省略し、形式を保持）。

5. 土圧係数 \( K_A \)

指針の土圧： \[ P_A = \frac{1}{2} \gamma H^2 K_A \]
土圧係数 \( K_A \) の公式（\(\omega\) を含む）： \[ K_A = \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \]
最適 \(\omega\) を代入すると、指針の \( K_A \)： \[ K_A = \frac{\cos^2(\phi – \alpha)}{\cos^2 \alpha \cos(\delta + \alpha) \left[ 1 + \sqrt{\frac{\sin(\phi + \delta) \sin(\phi – \beta)}{\cos(\delta + \alpha) \cos(\alpha – \beta)}} \right]^2} \]

追加説明

「微分 \(\frac{dP}{d\omega} = 0\) を解く（詳細は省略し、形式を保持）」の意味
土圧 \( P \) は滑り面の角度 \(\omega\) に依存しており、クーロン土圧では最大土圧を与える \(\omega\)（最も不安定な滑り面）が必要。そのため、\( P \) を \(\omega\) で微分し、導関数をゼロに設定（\(\frac{dP}{d\omega} = 0\)）して極値（最大値）を与える \(\omega\) を求める。この方程式を解くことで、最大土圧に対応する滑り面角度が得られる。
例：\( P = \frac{1}{2} \gamma H^2 \cdot \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \) の \(\omega\) 依存部分を \( f(\omega) = \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \) とし、\(\frac{df}{d\omega} = 0\) を解く。商の微分則や連鎖律が必要で計算は複雑だが、このプロセスが最大土圧の \(\omega\) を求める意味。
「最適 \(\omega\) を代入する」の意味
微分 \(\frac{dP}{d\omega} = 0\) で求めた \(\omega\)（最大土圧を与える滑り面角度）を \( P \) または \( K_A \) の式に代入すること。これにより、最大土圧 \( P_A \) と対応する \( K_A \) が得られる。指針では、この \(\omega\) は解析的に解かれ、以下の形式になる： \[ \omega = \tan^{-1} \left( \sqrt{\frac{\sin(\phi + \delta) \sin(\phi – \beta)}{\cos(\delta + \alpha) \cos(\alpha – \beta)}} \right) + \frac{\alpha + \beta + \phi – \delta}{2} \] 例：この \(\omega\) を \( K_A = \frac{\cos(\alpha – \beta) \cos(\omega – \alpha) \sin(\omega – \phi)}{\cos^2 \alpha \sin(\omega – \beta) \cos(\omega – \phi – \alpha – \delta)} \) に代入すると、指針の \( K_A = \frac{\cos^2(\phi – \alpha)}{\cos^2 \alpha \cos(\delta + \alpha) \left[ 1 + \sqrt{\frac{\sin(\phi + \delta) \sin(\phi – \beta)}{\cos(\delta + \alpha) \cos(\alpha – \beta)}} \right]^2} \) に一致する。

適用される構造物

　クーロン土圧を適用する構造物はかなり多いです。擁壁、橋台、自立式鋼矢板護岸などほとんどがクーロン土圧ではないかと思われます。
　ランキン土圧を適用する構造物については「次回のランキン土圧について解説」で解説いたします。

まとめ

　クーロン土圧理論では、主動土圧係数の算出方法は土の重量とすべり面と壁背面の反力のつり合いから導出されていることがわかりました。
　「クーロン土圧公式と試行くさび法をくらべてみた」でも述べた通り、試行くさび法はこのクーロン土圧の理論を拡張させたものであり擁壁の背面形状が複雑な場合でも計算が可能です。試行くさび法は微分するのではなく、ωを変えて繰り返し計算し最大となる土圧を導くものです。したがって同じことをアナログ的に実施しているということになります。
　このクーロン土圧理論はシャルル＝オーギュスタン・ド・クーロン（Charles-Augustin de Coulomb 1736年6月14日 – 1806年8月23日）により提唱されました。彼はフランス人で1776年にフランス科学アカデミー論文にこの理論を提唱しました。いまから約250年も前です。日本では江戸時代の十代将軍徳川家治の頃です。この時代にこのような考えが生まれ、これ以来ずっと変わらずこの理論が世界で受け継がれていることに驚くとともにこの理論の完成度の高さがうかがえます。