水路の粗度がなぜ断面全体の抵抗になるのか？ 乱流による摩擦伝達とマニング公式の秘密

　水が流れる河川や水路の水が接する壁面や水路底では粗度係数により流体に抵抗が生じて粗度係数が大きいほど流速が遅くなるのは周知のとおりですが、壁面や水路底から少し内側に入れば粗度の影響はなくなって流速にはあまり関係がないのではないか？と思ったことはないでしょうか。（私だけでしょうか(>_<)）
　それに関連することなのですが、平均流速公式である有名なマニングの公式があると思いますが、どうして「平均」とよばれるのでしょうか。また、何の平均なのかと思ったことはないでしょうか。さらにマニング式は実験式ですがなぜ理論式ではないのか、 私はそのように思った疑問から解説したいと思います。

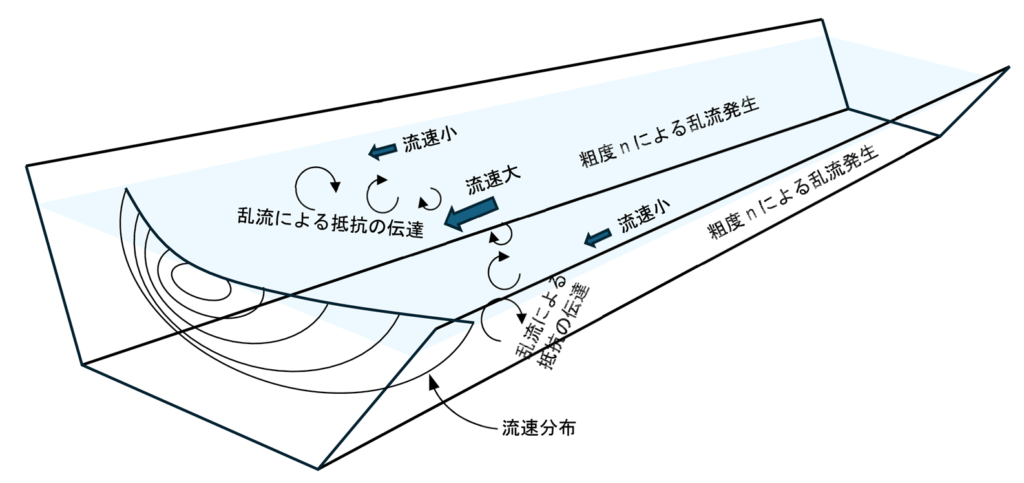
粗度による抵抗力は流れの中心に向かって伝わる

　冒頭に述べた、壁面から少し内側は粗度がないので影響はすぐ途切れるのでは？という疑問に対しては、実は粗度の影響は「壁面から流れの中心部に向かって伝わっていく」ということなんです。そのメカニズムとしては、まず、水など液体には「粘性」があります。液体の分子同士が引っ張り合っていることから生じています。この壁面での分子粘性によってせん断応力が生じ、壁面近傍ではそのせん断応力によって粗度に応じた乱流が生成され（分子粘性は粗度の大小に関係はない）、乱流による運動量輸送によって壁面粗度の影響が流路全体に伝達されます。せん断応力は厳密には流れの中では粘性と乱流によるせん断応力の合計ですが乱流によるものが卓越しています。
　したがって、粗度は水路断面全体の流速へ影響するということになります。

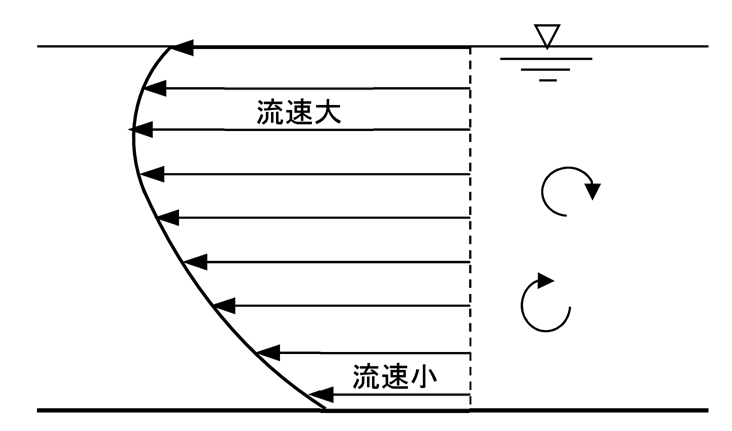
　上図のように壁面（底面）近傍では乱流の影響が強く、断面の中央に向かって影響が弱まるため中央部の流速が最も大きくなります。
　また、水路中央部を水路縦断方向にみた断面でみると水面より少し下の流速が最も早くなります。これは今調べ中ですが「自由水面が完全な無せん断境界ではないこと」「幅水深比が小さい水路では側壁に起因する二次流がこれを助長」が関係しているようです。

平均流速公式は何が平均なのか

　平均流速公式である有名なマニング公式ですが、何の平均なのか？の問いに対してはもうお分かりですね。
　開水路では底面や側壁の摩擦により断面内に流速分布が生じるため、流量計算や設計では、断面積で平均した代表的な流速として平均流速を用います。
　この断面積平均流速を与えるのが平均流速公式です

マニング公式はどうして実験式なのか

　マニング公式は、開水路乱流の抵抗機構が極めて複雑であり、特に粗度の影響を理論的に一意に表現できないため、実験・観測データに基づいて構築された実験式です。
　公式の形自体は次元解析や乱流理論と整合するのですが、粗度係数 n は経験的に定めざるを得ず、この点がマニング公式が実験式と呼ばれる本質的理由です。

コラム：円筒分水槽で流量を等分できる理由

　農業用水路などで複数方向に水を分ける場合、「断面積を同じにすれば流量も同じになる」と直感的に考えてしまいがちです。しかし実際の流れでは、水路断面内の流速分布は一様ではなく、単純に幅や開口を等分しただけでは流量を等しく分けることはできません。これは、先に述べた粗度による抵抗の違いや流速分布の偏りが原因です。

断面を等分しても流量は等分されない

　例えば、矩形断面の水路を仕切り板で左右に分けた場合を考えます。
・側壁付近は流速が遅い
・中央付近は流速が速い
このため、どこを切り取るかによって、同じ断面積でも通過する流量は異なります。
　つまり、

「形を等しく分ける」
≠
「流量を等しく分ける」

ということになります。

円筒分水槽という解決策

　この問題を解決するために考え出されたのが円筒分水槽です。円筒分水槽では、サイフォン⚠️で流れを一度円筒内に導き、中央から湧水させ
・流路を急激に拡幅する
・流速を低下させる
・流速分布の偏りを弱める
という操作を行います。
その結果、
分水部では流速の影響が小さくなり、主に**水位（静水圧）**によって流量が決まる状態になります。その結果、円筒の周囲ではどの位置でも水位がほぼ同じになります。
このため、どこから水を取り出しても、同じ条件で水が流れ出し、流量が等しく分配されるのです。

写真：富山県魚津市 東山円筒分水槽（筆者撮影）
日本一美しい円筒分水槽（国の登録有形文化財（建造物））　1955年完成　とやま観光ナビより

　円筒分水槽は、歴史的には古い分水施設ですが、水理学的には極めて合理的な構造を持っています。ただし、現代の土地利用や用水管理条件には必ずしも適合しないため、新設では簡素な定量分水工やゲート制御方式が主流となっています。
⚠️サイフォンとは、管路内を満水状態で流下させ、水位差（落差）による圧力を利用して、途中で高い位置や低い位置を経由して水を導く導水施設である。河川横断や谷部通過など、開水路では困難な地形条件で用いられる。

まとめ

　開水路の流れでは、底面や側壁の粗度によってせん断応力と乱流が発生し、その影響は断面内の一部にとどまらず、運動量輸送を通じて流路断面全体に及びます。
　このため、流速は断面内で一様とはならず、位置によって異なる分布をもつようになります。
　設計や流量計算では、このような分布をもつ流れを一点の流速で扱うことはできないため、断面積で平均した代表値として「平均流速」が用いられます。
　マニング公式は、この断面積平均流速を与える実用的な式であり、粗度の影響を理論的に一意に表現できないことから、粗度係数 n を経験的に定める実験式として位置づけられています。
　つまり、粗度による抵抗の伝播、流速分布の発生、平均流速の必要性、そしてマニング公式の経験的性格は、いずれも開水路乱流の本質に基づく一連の現象として理解することができます。

参考文献

　　　・絵解き水理学 改定第4版（オーム社）
　　　・大学土木 水理学改定2版（オーム社）
　　　・水理学詳説（理工図書）
　　　・農業水利（文部省）
　　　・土木公式活用ポケットブック（オーム社）