今回は前回のクーロン土圧論に続いてランキン土圧論について解説いたします。
ランキン土圧論
ランキン土圧の前提条件は以下になります。
①粘着力ｃ＝0
②内部摩擦角 φ ≠ 0°
③壁面摩擦角 δ ＝ 0°
④壁面傾斜 α ＝ 0°
⑤地表面傾斜 β ≥ 0°
⑥すべり面 固定角度ω＝45°＋φ／2
⑦解析方法 モール円による応力解析
⑧破壊基準 τ＝σtanφ
⑨土圧係数 KA φ、βに依存
⑩土圧の作用方向 水平（壁面に垂直、βに影響なし）
⑪上載荷重 q = 0
ランキン土圧について、下図のようなケースを想定してみます。
図ー１ 主動状態の壁と土の挙動
図ー２ 土圧の作用
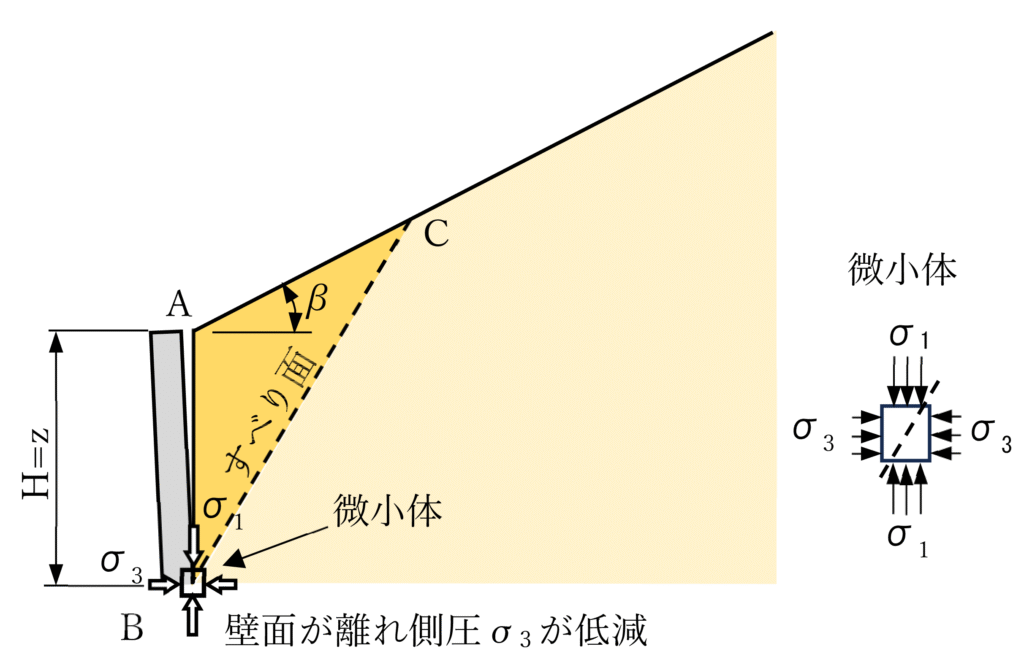
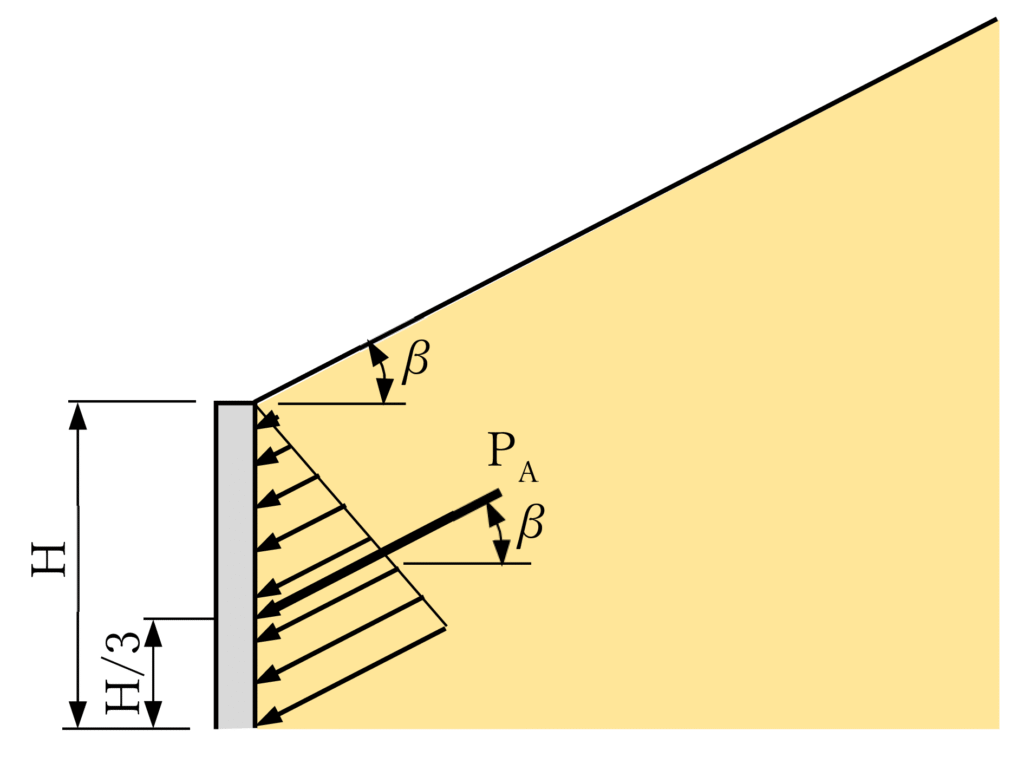
擁壁が背面土からわずかに離れる（主動状態）と、壁に接する土中の応力状態を考えます。図－１のように、壁の下端（深さz =5.0m）にある土の微小体（小さな土の部分）に、鉛直応力σ1=γz（γは土の重さ、( z )は深さ）と、水平方向の土圧σ3が作用するとします。 主動土圧係数 Ka ＝σ3/σ1 で定義されるとします。微小体の応力をモールの応力円で表すと、壁を土から離す（主動状態）では、σ3 が減少し、応力円の直径（σ1−σ3）が大きくなるとします。応力円が破壊基準（τ=σtanϕ φは土の強さの指標）に接する点で土が破壊し、水平から45°＋φ／2のすべり面が生じます。その時の σ3/σ1 が主動土圧係数 Ka となります。地表面に傾き（β）がある場合、σ3 はβを考慮したKAにより計算され、KAはβと内部摩擦角φを用いた式で与えられます。
図ー３ モールの応力円
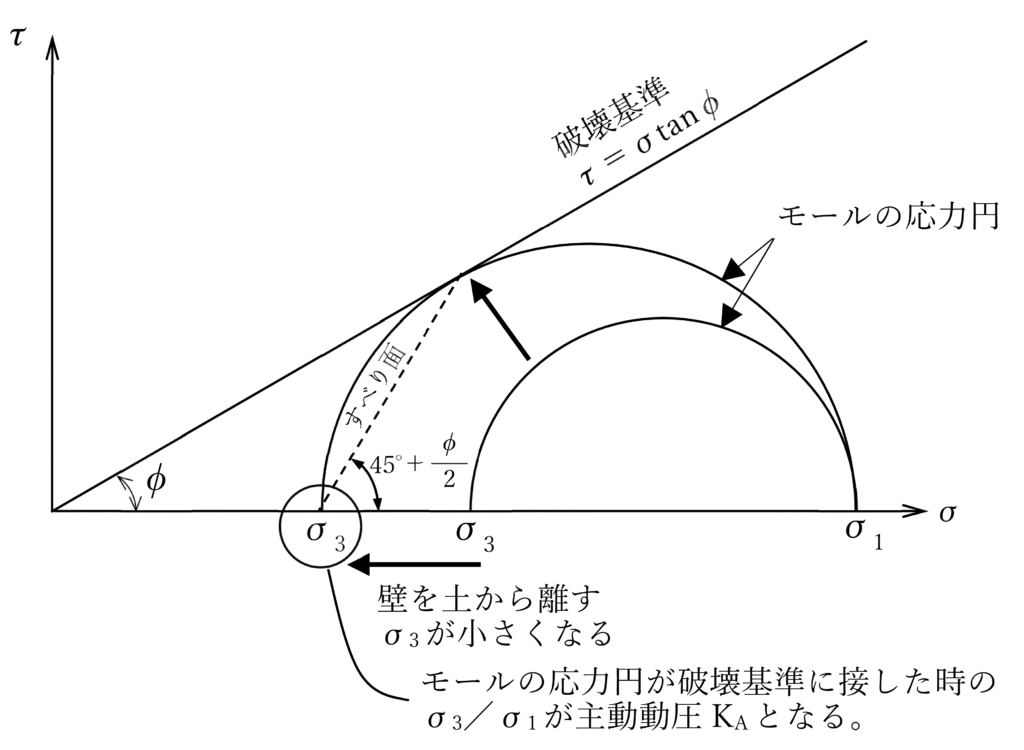
ランキン土圧による最大土圧の算出
ランキン土圧は前述の考えより下式で表すことができます。
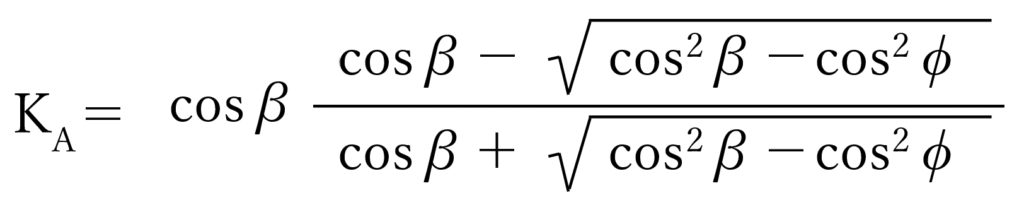
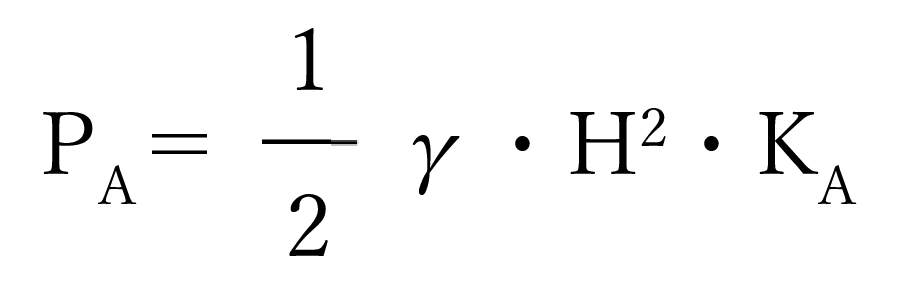
導出過程は複雑なため省略。
なお、β＝0の場合では最大土圧となるωとKAは以下のようにクーロン（α＝0、β＝0、δ＝0の場合）と同じになります。
ランキン土圧理論では、土が壊れるとき、滑り面は水平から45°＋φ/2の角度で生じるとします。（φは土の強さの指標）。例えば、φ＝30°なら、すべり面は45°＋15°＝60°です。地表面に傾きβ（例：β＝10°）があっても、すべり面角度は45°＋φ/2のままで、βの影響は土圧係数KAに反映されます。れに対し、クーロン土圧では、壁面摩擦δやβにより滑り面角度が変わり、たとえばδ=20°でω≈55°となります。
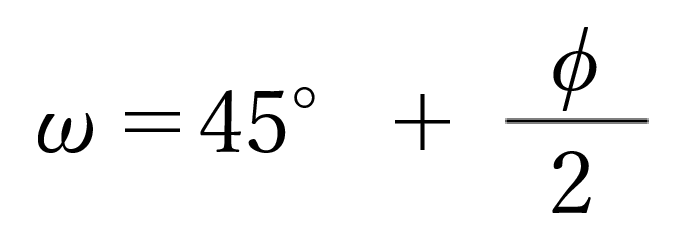
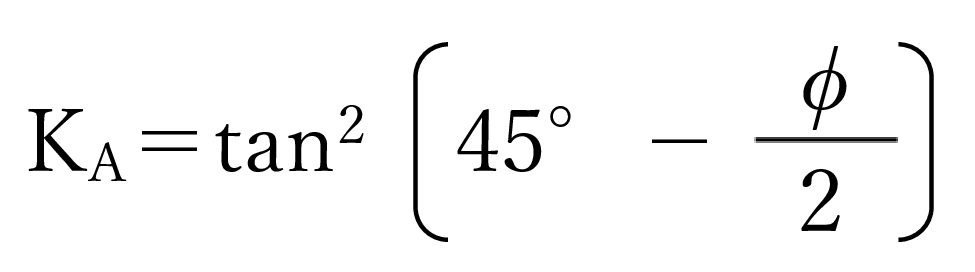
適用される構造物
ランキン土圧を適用するのは切梁式土留における土留め壁に対する土圧算出です。道路土工仮設工指針の切梁式土留の設計における主動土圧係数は壁面摩擦角を考慮しない式として上記のKAの式が記載されています。
まとめ
ランキン土圧理論では、主動土圧係数KAがモールの応力円と破壊基準（τ＝σtanφ）を使って導出されていることが分かりました。例えば内部摩擦角φ＝30°、地表面傾斜角β＝0°の場合、KA＝0.3333、壁底で土圧σA＝31.67kpa、合力PA＝79.18kN/mとなり、土圧は水平に作用します。この理論はウィリアム・ジョン・マクォーン・ランキン（William John Macquorn Rankine 1820年7月5日 – 1872年12月24日）により提唱されました。彼はイギリス人で1857年に論文「On the Stability of Loose Earth」を発表し、土圧理論を提唱しました。彼はクーロンの提唱（1776年）より約80年後に、土の応力場を数学的に解析する方法を確立しました。ランキンの特徴は、壁面摩擦が無い（δ＝0°）前提で、すべり面が常に水平から45°＋φ／2となる点です。地表面傾斜βがあってもすべり面角度は変わらず、βの影響はKAに反映されます。（クーロンはδを考慮しすべり面角度は変動）
ランキンは、壁摩擦が無視できる簡単な擁壁や仮設土留め、土圧の基本を学ぶ教育で役立ちますが、実際の複雑な擁壁ではクーロンや拡張式が使われます。粘着力（ｃ≠0）や上載荷重（ｑ≠0）を考慮した拡張式もあり、現代の土木工学で柔軟に対抗可能なように進化されています。モール円を使った視覚的な説明は、土の力の動きを直感的に理解するのに最適です。
