こんにちは。今回は不等流計算を単純な四角形の水路断面で断面の計算ピッチを変えて計算すると、どのような違いが出るのかを確認してみることにしました。計算ピッチは1.0mと10.0ｍのケースとしました。
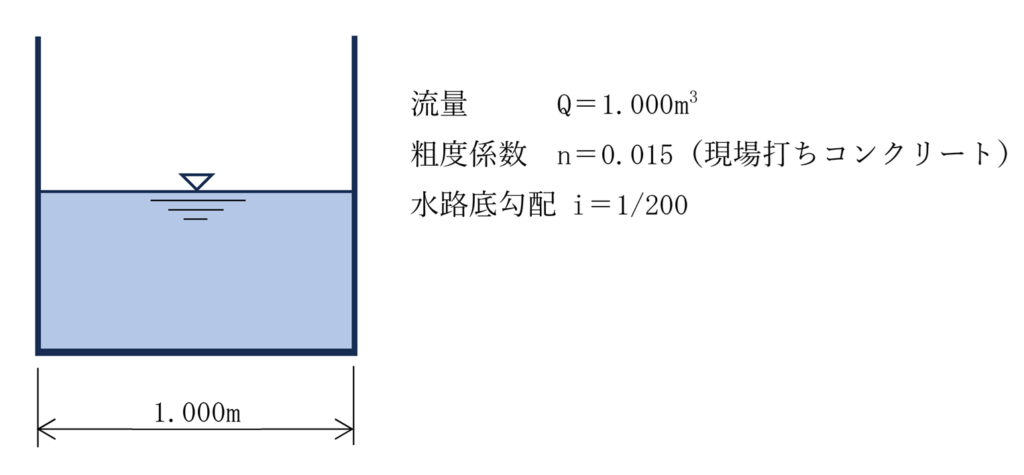
計算する水路断面は水路幅1.0mで、現場打ちコンクリートとしてみたいと思います。また、水路勾配は1/200とします。これに流量Q=1.000m3/sを流すこととしましょう。なお、別途計算してこの条件では「常流」になりました。
常流なので、不等流計算は最下流の水深を設定して計算を行いたいと思います。最下流の水深はとりあえず、限界水深としましょう。限界水深は上の写真の水路に段差があるところの上の段で水が落下する位置の水深で、計算する水路の下流の水深として設定しやすいものになります。
限界水深は以下のように0.467mになります。
まず、計算ピッチを1.0ｍと細かく設定して不等流計算をしたときの水面形がどうなるか計算してみます。計算は「土地改良事業計画設計基準及び運用・解説 設計「水路工」」に記載の逐次計算法にて行うことにします。
計算は水面が概ね収束する70ｍまで行いました。最下流の水深は測点0で先ほどの限界水深としています。
中間部は割愛
グラフにすると水面形が分かりやすくなります。このようにきれいな曲線になりました。
次は10.0mピッチです。
水面形は10m地点で折れた線になっています。
次に等流水深を算出しておきます。不等流計算をして上流側で収束する水位は等流水深になると言われていると思いますが、ついでにそれも確認してみたいと思います。等流水深はマニングの式で水深を繰り返し値を変えて計算して流量が条件の1.0m3/sになる水深を確認しました。等流水深の計算結果は0.526mになり不等流計算結果の最上流水深と一致しました。
計算ピッチを1.0mと10.0mで変えて計算してみまして分かったことを下記に記載します。
・計算ピッチ1.0ｍでは下流側の10.0ｍの範囲で水面形が大きく変化することが分かりました。また、きれいな曲線を描いており良い計算ができたと思います。
・計算精度は1.0mピッチでは計算回数が多くなるので、最初の予想では上流側の水深の精度が低下すると思いましたが、等流水深である0.526mにきちんと計算されました。これは誤差を極力小さくすれば精度は確保できるものだと思います。
・計算ピッチ10mでは、下流での水面形が粗く10ｍ地点で折れ線グラフのようになっていまして、計算ピッチ1.0mとは計算誤差が大きくなります。（といっても、このケースでは1cmしか変わりませんが）グラフを比べると計算ピッチ10.0mでは良い計算をしたとはいいにくいですね。
・計算ピッチ10mでは、これでも上流側の水深はきちんと0.526ｍと等流水深になりました。このことから、最上流の水深を計算する際には計算ピッチは今回のケースでは差はみられないということになりました。ただし、最下流位置から等流水深になる距離は1ｍピッチでは52ｍですが、10ｍピッチでは20mとかなり違いが見られました。下流側の計算結果は精度が悪そうですね。
今回は計算ピッチを変えて水路断面での不等流計算を実施してみました。計算ピッチを数多く設定すると精度は高くなりますが計算や断面条件の入力手間がかかりますし極力効率よくしたいところですね。今回のように、常流で下流水深を限界水深として計算する場合には下流はピッチを細かく設定し、上流は粗く設定するなどでも良いのではないでしょうか。
私の経験では水路ではなく河川不等流が多いのですが、河川では仮設の締め切り高さを設定するのに計算します。締め切りのわりと近い下流位置で出発水位を設定し、近くで締め切りの変化点ごとに計算位置を設定しますので短い区間で計算ピッチを設定していると思います。その代わり締め切りより上流側では粗いピッチで計算しています。
最後まで読んでいただきありがとうございました。
個人向け総合通販「よろずやマルシェ」
“あの”リンパマッサージセルライトスパッツに待望の男性シリーズ登場！
医師も推奨ショップ！減塩なら減塩専門店「無塩ドットコム」の初回限定・8種調味料セット！
