鉄筋コンクリート構造や鋼構造などではフックの法則に基づいたヤング係数を用いて構造検討を行いますが、これらについて概説し、これらがどのように設計で用いられるのかを解説いたします。
フックの法則とヤング係数の起源
フックの法則は、ロバート・フック（Robert Hooke, 1635–1703）が発見した経験則で、弾性限度内で「力と変形が比例する」ことを示します。例えば、ばねに加えた力（F）とその伸び（x）が比例し、F = -kx（kはばね定数）で表されます。フックはこれを言葉で記述し、現代の数式形式では表現していませんでした。 材料力学では、フックの法則は応力（σ）とひずみ（ε）の比例関係（σ = Eε）として表現されます。この比例定数Eはヤング係数（Young’s modulus）と呼ばれ、材料の剛性を示します。トマス・ヤング（Thomas Young, 1773–1829）は弾性率の概念を導入し、材料の弾性特性を定量化する基礎を築きました。この数式は、ヤングの貢献をもとに、その後の科学者たち（特に19世紀の材料力学の発展期に）によって体系化されたものです。
フックの法則
フックの法則ついて以下に式を示します。
E = σ ε
または σ = Eε
ここに、
σ：応力度（N/㎜2）
ε：ひずみ（無次元）
E：ヤング係数（または弾性係数）（N/㎜2）
ヤング係数Eは材料固有の数値で同じ材料では一定です。
応力（σ）とひずみ（ε）
フックの法則で用いられる応力（σ）とひずみ（ε）の説明をします。
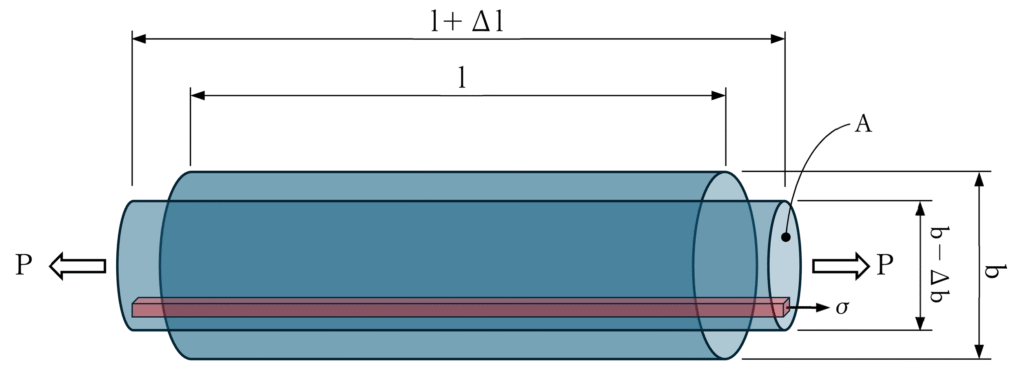
下図に示すように長さlの円筒形の物体について外力Pなる引張を作用させたとすると長さはΔlだけ伸びます。その時の応力（σ）とひずみ（ε）として以下のように表します。
σ = A P
ここに、
σ：応力度 A：断面積 P：外力
ε = Δl l
ここに、
ε：ひずみ Δl：伸び量 l ：物体の長さ
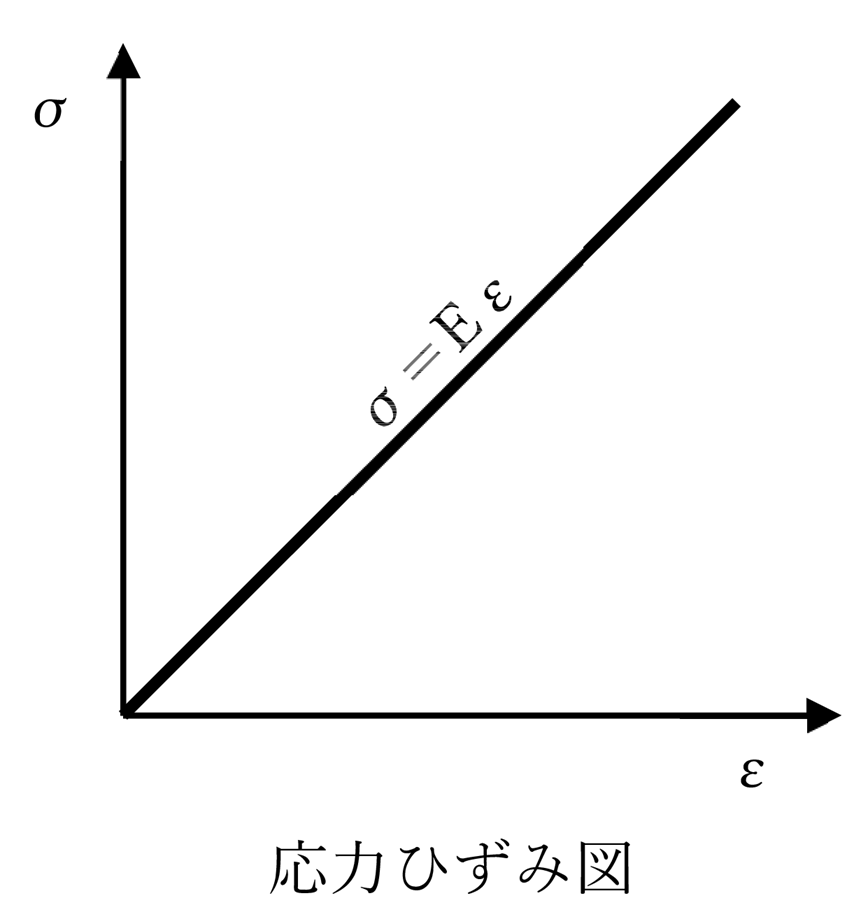
また、応力とひずみの関係の概念をグラフで表すと以下のようになり、ヤング係数（E）は応力ひずみ関係の傾きを表すものでもあります。実際のグラフは単なる直線ではありませんが、理解のため簡単な図で表します。
そして、再掲になりますがヤング係数（E）は応力（σ）とひずみ（ε）の式として以下になります。
E = σ ε
または σ = Eε
これより、材料により同じ外力でも硬い材料はひずみが小さくヤング係数が大きくなります。柔らかい材料はひずみが大きくヤング係数が小さくなります。
ヤング係数の事例
以下にヤング係数の事例として鉄筋とコンクリートのヤング係数を記載します。鉄筋の方がかなり硬いということになります。
| 項 目 | ヤング係数（Es） （N/㎜2） |
| 鋼（鉄筋含む） | 2.0 × 105 |
| コンクリートの 設計基準強度 | ヤング係数（Ec） （N/㎜2） |
| 21 | 2.35 × 104 |
| 24 | 2.5 × 104 |
| 27 | 2.65 × 104 |
| 30 | 2.8 × 104 |
| 40 | 3.1 × 104 |
| 50 | 3.3 × 104 |
| 60 | 3.5 × 104 |
H29道路橋示方書Ⅲコンクリート橋・コンクリート部材編より
ヤング係数の利用
上述のヤング係数（E）は、土木設計において大変重要な役割があります。その一例として、鉄筋コンクリート構造の解析になります。従来より許容応力度法における鉄筋コンクリート構造では以下の仮定がなされます。
（１）維ひずみは中立軸からの距離に比例する
（２）コンクリートの引張強度は無視する。
（３）鉄筋とコンクリートのヤング係数比は15とする。
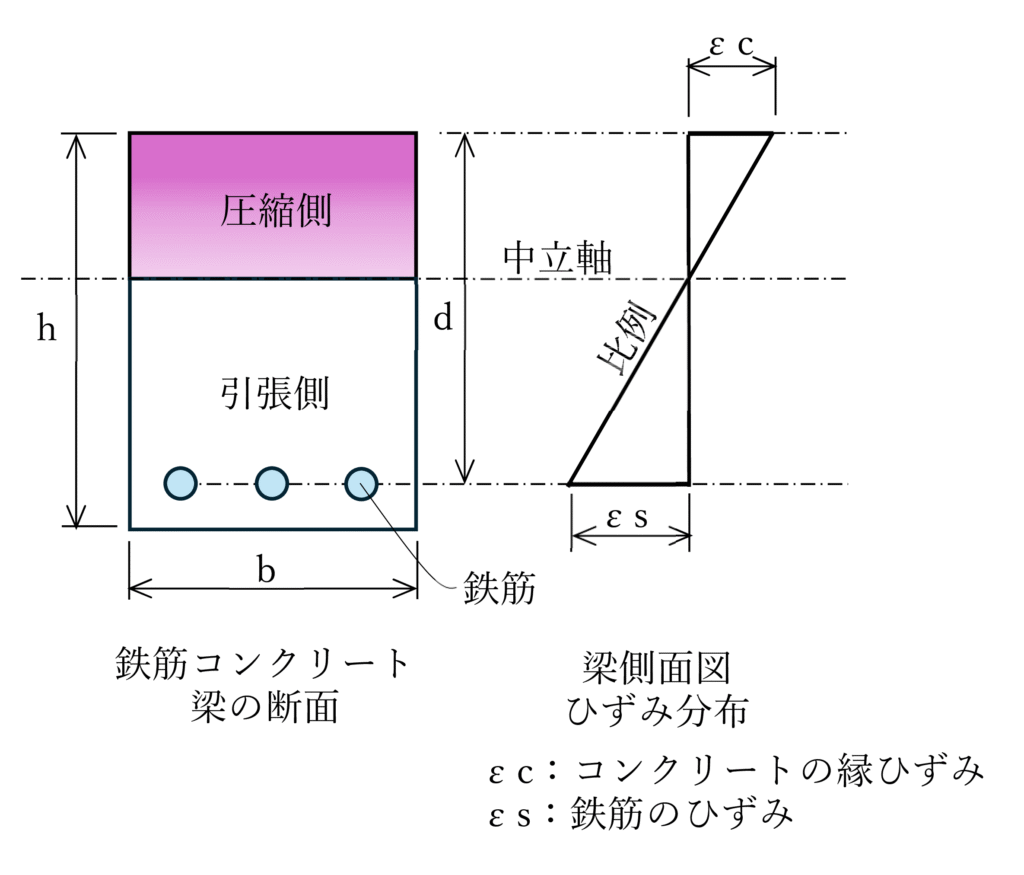
（１）は、違う言い方をすると「部材断面のひずみ分布は平面保持則に従う」というものです。平面保持則とは、曲げによって部材が曲がっても、断面のひずみ分布は平面を保持すると言う意味です。
中立軸とは断面内で伸びも縮みもしないひずみが0（と同時に応力が0）となる位置であり、中立軸からの距離が離れるとひずみ分布は比例して大きくなるとしてよいということです。
（２）はコンクリートは一般的に引張強度は非常に小さいので無視するということです。
（３）は、断面に曲げが生じると中立軸より引張側の鉄筋が負担する力Tと圧縮側のコンクリートが負担するCの値は同じと考えますが、そうなるような基準となる中立軸の位置を決める必要があります。その中立軸の位置には引張側は鉄筋なので同じ応力度の絶対値でもひずみが小さく、圧縮側は同じ応力度の絶対値でもひずみが大きくなります。またそれぞれの負担する面積も考慮することになります。したがって、平面保持則から比例計算により鉄筋とコンクリートのようにヤング係数の値が異なる場合の比を中立軸の算定に考慮して計算し、それぞれの材料に働く応力度を算定します。
許容応力度法では鉄筋とコンクリートのヤング係数の比をヤング係数比ｎ＝Es／Ec＝15として計算に利用しています。
このn=15という値は、昭和時代からある値であり昭和の文献を読むと鉄筋のヤング係数は2100000kg/fcm2でコンクリートが140000kgf/cm2ということから設定されているようです。コンクリートのヤング係数はかなり低めに設定されたまま現在まで使われていることになりますね。
今後は限界状態設計法が主流になりつつあるので鉄筋とコンクリートそれぞれに指定された応力ひずみ図を用いることが多くなると思われます。
終わりに
以上、フックの法則とヤング係数について、その基本的な概念から鉄筋コンクリート構造の設計における実際の利用まで解説しました。ヤング係数は、材料の剛性を定量化し、構造物の安全性を確保する上で欠かせない要素です。特に、鉄筋コンクリート構造では、平面保持則やヤング係数比（n = 15）を活用した中立軸の算定が、効率的かつ安全な設計に直結します。昭和時代から続くn = 15という値は、現代の設計においても簡便な基準として活用されていますが、今後は限界状態設計法の普及に伴い、より詳細な応力-ひずみ関係に基づくアプローチが増えるでしょう。土木設計に関わる皆さんが、ヤング係数の理解を通じて、より安全で合理的な構造物を設計する一助となれば幸いです。
関連商品
この広告はアフィリエイトを利用しています。
