許容応力度法にて鉄筋コンクリート部材に発生するコンクリートと鉄筋の応力度を求めるための方法について解説します。
今回は曲げ応力度に対しての計算法や照査法を説明します。曲げ応力度とは梁などの部材が曲げられることによって断面内に引張側と圧縮側が生じてそれぞれの応力度を計算して照査するものです。一般的に曲げ応力度以外にはせん断応力度がありますが、それは別の機会とします。
目次 閉じる
中立軸位置の計算
下図のように梁に自重や車両などの外力によって鉄筋コンクリート梁に曲げモーメントが生じることを想定します。
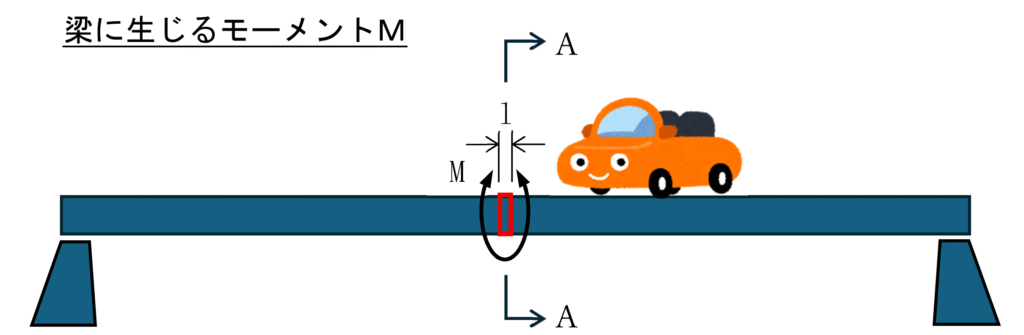
まず、梁における鉄筋コンクリート断面の中立軸位置の計算を行います。下記のように、平面保持則より条件1と、力のつり合いより条件2により中立軸係数kを算出することが重要になります。
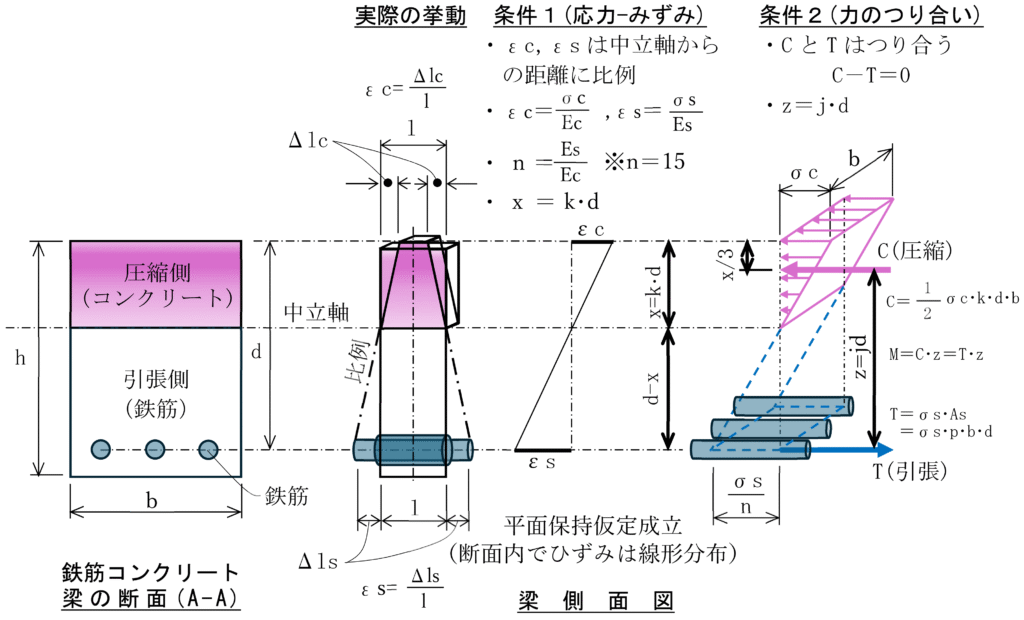
l :変形前の部材延長 (㎜)
Δlc:コンクリートの縮み量 (㎜)
Δls:鉄筋の伸び量 (㎜)
x :中立軸の位置 (㎜)
k :中立軸係数
z :レバーアーム
j :レバーアーム係数
εc:コンクリートの縁ひずみ (無次元)
εs:鉄筋のひずみ (無次元)
Ec:コンクリートのヤング係数(N/㎜2)
Es:鉄筋のヤング係数 (N/㎜2)
σc:コンクリートの応力度 (N/㎜2)
σs:鉄筋の応力度 (N/㎜2)
As:鉄筋の断面積 (㎜2)
中立軸位置xは中立軸係数kを乗じて算出する。そのためkの導出が主となる。
条件1より
ひずみと中立軸の位置関係を表すと
\[ \frac{\varepsilon_c}{\varepsilon_s} = \frac{x}{d – x} \]
ひずみεc,εsはEc,Esおよびσc,σsで表す。
\[ \varepsilon_c = \frac{\sigma_c}{E_c}, \quad \varepsilon_s = \frac{\sigma_s}{E_s} \]
これより、中立軸の位置関係をσs,σcとEs,Ecで表せる。
\[ \frac{\frac{\sigma_c}{E_c}}{\frac{\sigma_s}{E_s}} = \frac{E_s}{E_c} \frac{\sigma_c}{\sigma_s} = \frac{x}{d – x} \]
Es / Ec = nとしてまとめ、x = k d なので
\[ n \frac{\sigma_c}{\sigma_s} = \frac{k d}{d – k d}, \quad \frac{\sigma_c}{\sigma_s} = \frac{k}{n(1 – k)}, \quad k = \frac{n \sigma_c}{n \sigma_c + \sigma_s} \quad \text{・・・(1)} \]
条件2より
\[ C = \frac{1}{2} \sigma_c k b d, \quad T = \sigma_s A_s = \sigma_s p b d \]
コンクリート断面形状(b,d)と鉄筋量(As)はP(引張鉄筋比P= \(\frac{A_s}{b d}\) )に置き換える。
力のつり合い条件ΣH=0なので
\[ C – T = 0 \]
\[ \frac{1}{2} \sigma_c k b d – \sigma_s p b d = 0 \quad \text{・・・(2)} \]
(1)と(2)よりσcとσsも消えて、kはnとpのみで表すことができる。
\[ k^2 + 2 n p k – 2 n p = 0 \]
\[ k = \sqrt{2 n p + (n p)^2} – n p \]
最後に中立軸の位置xは
\[ x = k d \]
曲げ応力度の計算
外力によって生じる曲げモーメントより、コンクリートに生じる縁端の応力度σcと鉄筋の応力度σsを求める。
外力によって生じる曲げモーメントは断面に作用し以下の関係となる。
\[ M = C \cdot z = T \cdot z \]
また、レバーアームの長さを求めるための係数jを求める。
圧縮側の合力の作用位置は、圧縮側縁端から
\[ \frac{x}{3} = \frac{k \, d}{3} \]
であるから、
\[ z = j \, d = d – \frac{x}{3} = d – \frac{k d}{3} = \left( 1 – \frac{k}{3} \right) d \]
よって、
\[ j = 1 – \frac{k}{3} \]
したがって、
\[ M = C z = \frac{1}{2} \sigma_c b x \left(d – \frac{x}{3}\right) = \frac{1}{2} \sigma_c k j b d^2 \quad \text{・・・(1)} \]
\[ M = T z = \sigma_s A_s \left(d – \frac{x}{3}\right) = \sigma_s p j b d^2 \quad \text{・・・(2)} \]
(1)からσc、(2)からσsを求める。
\[ \sigma_c = \frac{2 M}{k j b d^2}, \quad \sigma_s = \frac{M}{p j b d^2} \]
応力度の照査
許容応力度法による照査
許容応力度法では上記より求めた応力度σc,σsが許容応力度σca,σsaを超えないことを確認することで安全な構造を満足するものと考える。
\[ \sigma_c \lt \sigma_{ca}, \quad \sigma_s \lt \sigma_{sa} \]
まとめ
本ブログでは、鉄筋コンクリート部材の設計における許容応力度法の考え方と計算手順を整理しました。まず、中立軸位置を求めるために中立軸係数 k を導出し、ひずみの関係や断面係数から中立軸位置を算出しました。次に、外力によって生じる曲げモーメントから、コンクリート縁端の応力度 σc と鉄筋の応力度 σs を計算しました。レバーアーム係数 j を使うことで、断面寸法と鉄筋量から具体的な応力度を求められることも確認しました。
そして、許容応力度法では、この求めた応力度 σc、σs がそれぞれ許容応力度 σca、σsa を超えないことを確認することで、安全な構造であることを保証できます。この手法は、複雑な非線形解析を行わずとも、断面設計と安全性照査を効率的に行えることが特徴です。
今回の流れを理解することで、許容応力度法を用いた鉄筋コンクリート設計の全体像が把握でき、設計の各ステップでどのように安全性を確認するかを理解することができます。
技術計算サイトの方にも計算するページを作成してみましたので、試してみてください。



