水理学では層流や乱流という言葉を聞くことがあると思います。また、これにはレイノルズ数という数も関わってきます。この言葉自体は聞いたことがあるのではないでしょうか。しかし、私自身これを設計で扱ったことはありません。では、これは何なのでしょうか。技術者の皆さんもそういえばという感じなのではないでしょうか。後の回でマニング公式に触れる前にこれの考え方の理解があると良いと思いまして解説したいと思います。
目次 閉じる
流体力学の古典的な実験に「レイノルズの実験」があります。1883年にオズボーン・レイノルズが発表したこの実験は、管の中を流れる水が「層流」になるか「乱流」になるかを、とても視覚的に示してくれます。
透明なガラス管に水を流し、入口付近から着色したインクを細く注入します。 水の流速を少しずつ変えながら、インクの様子を観察します。
流速が遅いと、インクはまっすぐな一本の線となって流れ、ほとんど混ざりません。流体が層のように整然と流れている状態でこれが層流です。

バルブを開けて流速を上げると、ある時点からインクが急に揺らぎ始め、すぐに管全体に広がって波状になり混ざります。渦が発生して不規則な流れになりこれが乱流です。

上記の層流と乱流を判断するのが有名な**レイノルズ数(Re)**です。
ここで、Re:レイノルズ数(無次元)
V :平均流速(m/s)
R :径深(m)(= 断面積 A(m2) / 潤辺 P(m))
ν :動粘性係数(m2/s)
Dh:水理直径(m)
D :直径(m)
上の式で求められたレイノルズ数から層流と乱流を判定するには以下のように言われています。(円管の場合)
Re<2000 :層流
2000<Re<4000 :過渡状態
4000<Re :乱流
※円管以外の一般形の値が示された書籍は見当たりませんでした。随時探してみます。
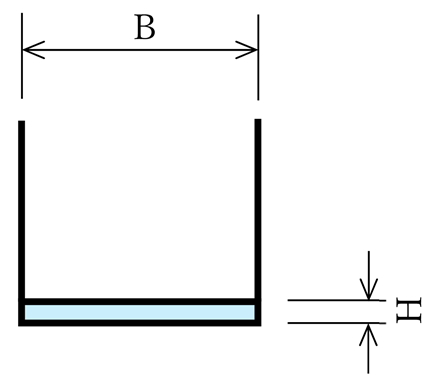
ここで、下記の断面についてレイノルズ数を算定してみたいと思います。上式からして流速を遅くするほうがレイノルズ数が小さくなりそうなので水深を1cmと極端に浅くし、水路勾配も0.3%と緩くします。どのようにになるでしょうか。
【条 件】
水 路 幅B :0.30 m
水 深H :0.01 m
粗度係数n:0.013
縦断勾配i :0.3 %
動粘性係数:1.146×10-6 m2/s(15℃)
【計算結果】
このようにレイノルズ数は6130と大きな値になりました。上記の層流と乱流の判断する指標の4000を大きく超えていますのでこのような小さな流速でも「乱流」ということでしょう。ちなみに水深を0.24mで計算するとレイノルズ数は277000になりとんでもなく大きな値になります。このことから、実際の土木設計で扱う水路や管路ではほとんどが乱流を想定したものになります。
いろんな書籍をみると、層流と乱流との限界となる流速を「限界流速」といい、流速の小さな状態から次第に大きくする場合(層流から乱流)と、逆に流速の大きな状態から次第に小さくしていく場合(乱流から層流)とによって限界流速は異なるということです。一般に前者の限界流速の方が大きい値となるという記述がありました。これと「絵とき水理学」記載のグラフも合わせてみると、私の推測ですが、これが2000<Re<4000の過渡状態なのではないかと思いました。私の調べではその明確な記述がありませんでしたので今後調べていきたいと思います。
あと、地下水の流れは層流が多いようです。土木設計ではこれらの限界流速やレイノルズ数自体を用いることはほとんどないと思いますが、知識として知っておくと思います。



