前回まではクーロン土圧論とランキン土圧論の解説をおこないました。今回は実際に計算をしてそれぞれの値がどのような傾向にあるのかを比較して確認したいと思います。
前提条件の比較
前回も記事の冒頭で提示しましたが、前提条件を比較しておきます。
ただし、現行の土木設計の指針・基準類とは異なる可能性があります。現行の土木設計の指針・基準類では拡張された式を採用されていることが多いためです。下記は拡張されていないクーロン、ランキンについて示しています。
| 項 目 | クーロン | ランキン | 違いがある項目 |
| 粘着力ｃ（kN/m2） | ｃ＝0 | ｃ＝0 | |
| 内部摩擦角φ（°） | φ ≠ 0° φ > β | φ ≠ 0° φ > β | |
| 壁面摩擦角δ（°） | δ ≠ 0° | δ ＝ 0° | 〇 |
| 壁面傾斜α（°） | α ≥ 0° | α ＝ 0° | 〇 |
| 地表面傾斜角β（°） | β ≥ 0° β < φ | β ≥ 0° β < φ | |
| すべり面最大土圧の 角度ω（°） | ω ≈ 55° | 固定角度ω＝45°＋φ／2 | 〇 |
| 解析方法 | 滑動くさびのつり合い | モール円による応力解析 | 〇 |
| 破壊基準 | τ＝σtanφ | τ＝σtanφ | |
| 土圧係数KA | φ、δ、α、βに依存 | φ、βに依存 | 〇 |
| 土圧の作用方向 | 壁法線からδ° | 水平（壁面に垂直、βに影響なし） | 〇 |
| 上載荷重ｑ（kN/m2） | q = 0 | q = 0 |
計算ケースの比較
計算するケースは形状が同じとします。ランキンでは前提条件が壁面傾斜αは考慮できないのでクーロンも０°とます。地表面傾斜角βを変えた2ケースと、3ケース目に参考としてクーロンの前提条件で本来考慮すべき壁面摩擦角δを0°として計算してみます。
ケース１ 法面あり：α＝0° β＝26.565° クーロンδ＝20° ランキンδ＝0°
ケース２ 法面なし：α＝0° β＝0° クーロンδ＝20° ランキンδ＝0°
ケース３ 法面なし、クーロンの壁面摩擦角なし【参考】
※クーロンの前提条件はδ ≠ 0であるため参考計算
α＝0° β＝0° クーロンδ＝0° ランキンδ＝0°
※26.565°は2割の法面勾配 20°＝2/3φ φ＝30°
α＝0° β＝26.565° クーロンδ＝20° ランキンδ＝0°
| 項目 | クーロン | ランキン |
|---|---|---|
| 略図 |  |  |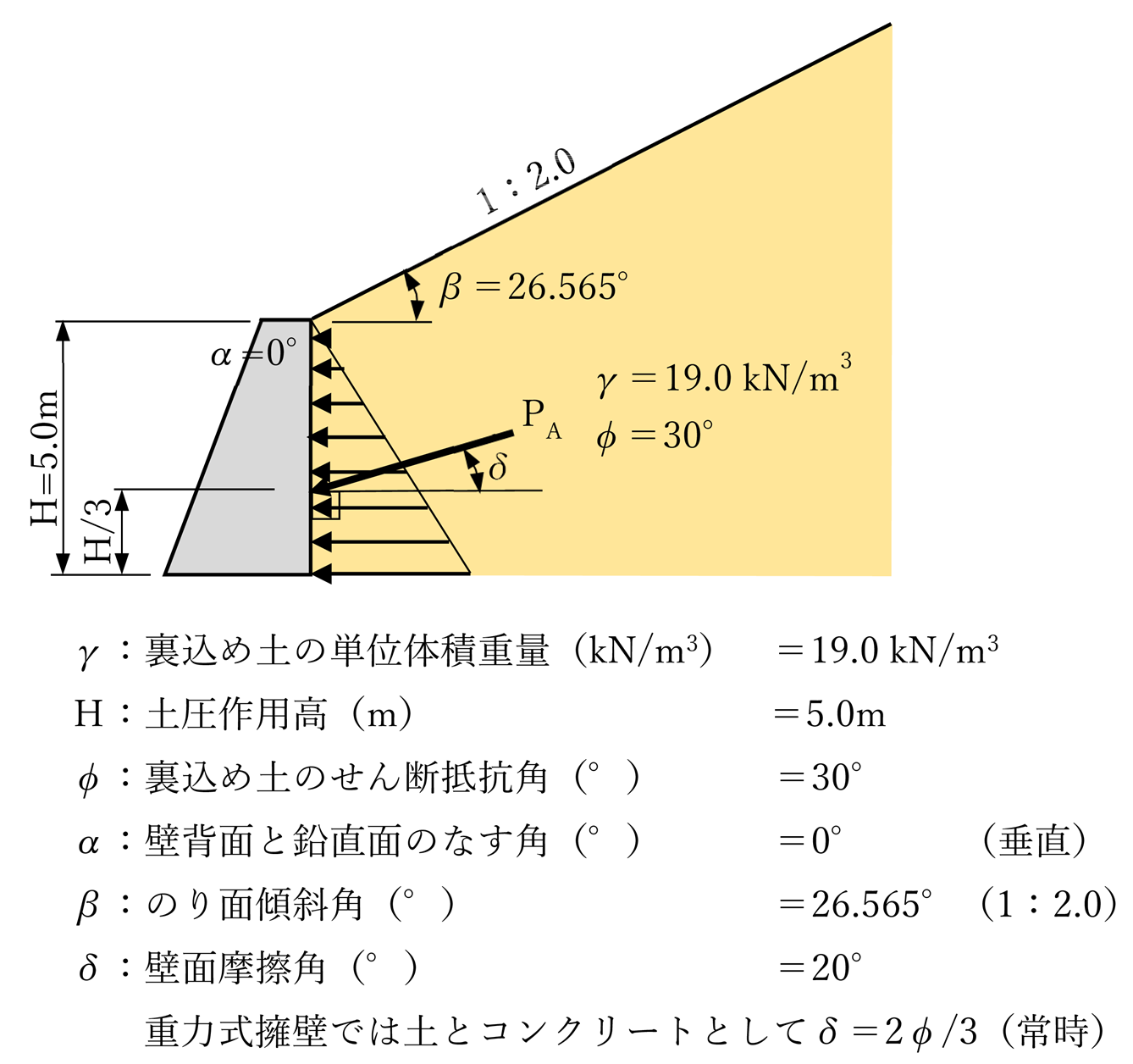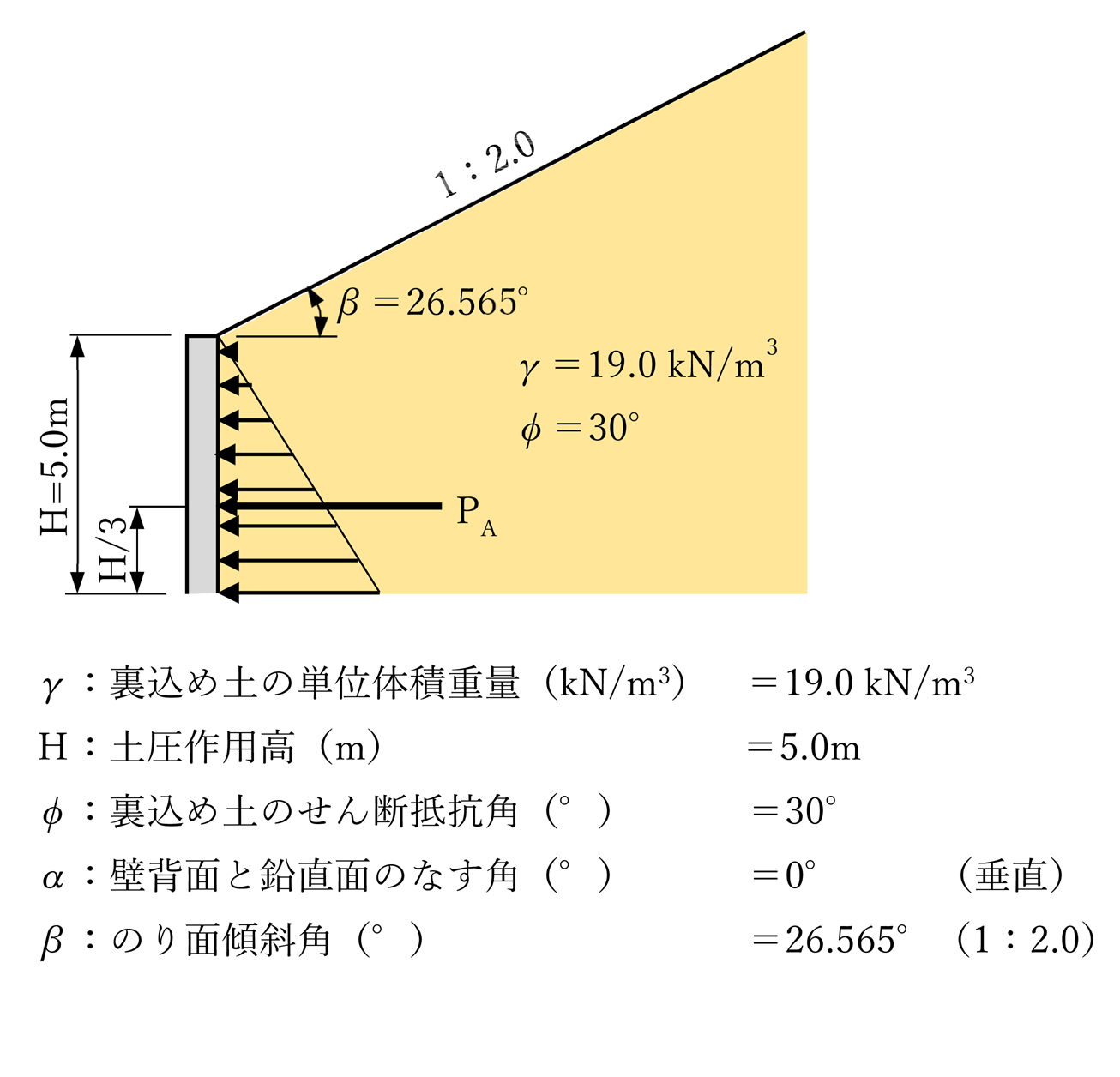
| 計算式 |  |  |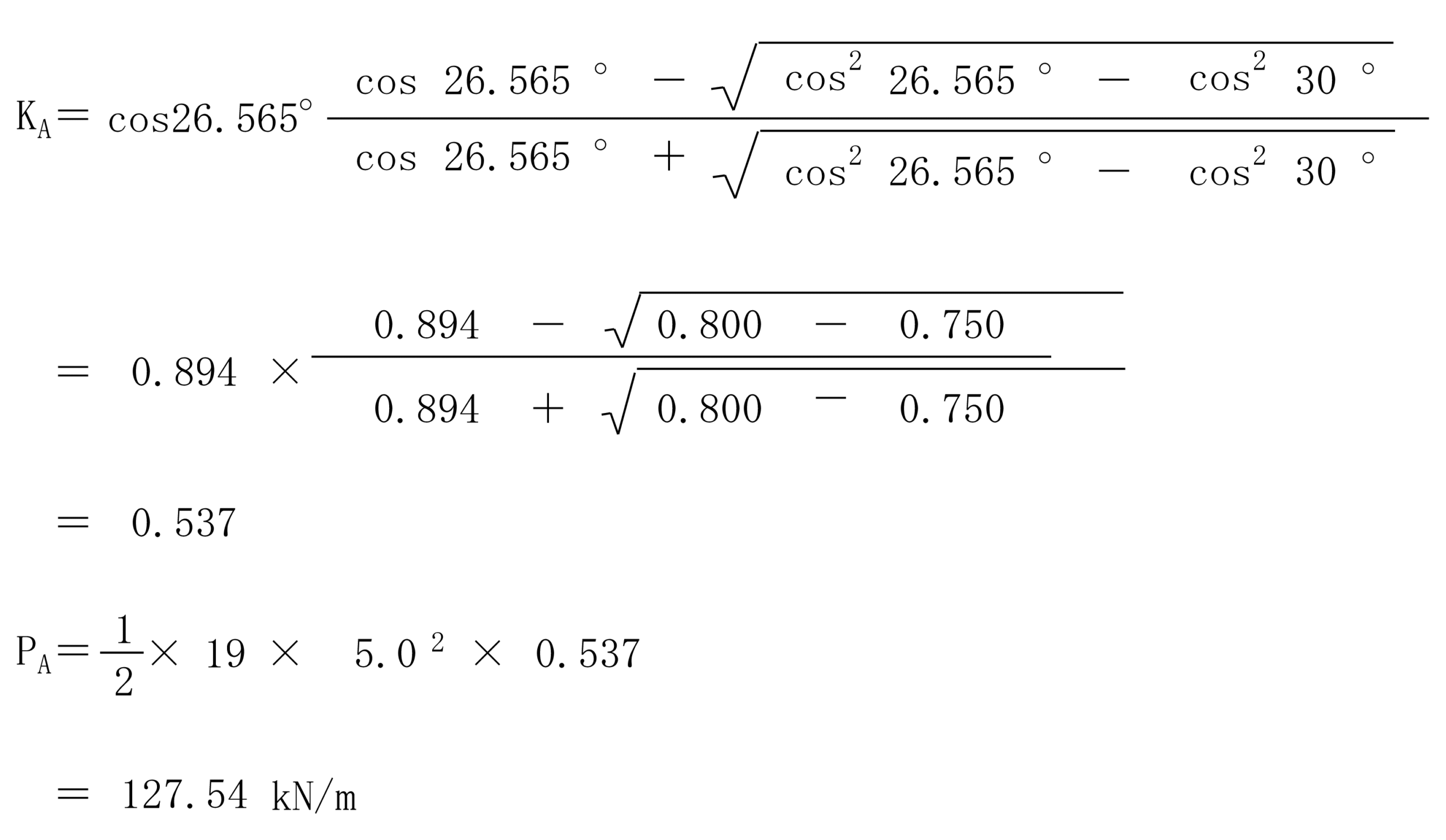
| 結果 | PA＝124.45kN/m | PA＝127.54kN/m |
| 評価 | ランキンの主動土圧が若干（2.4％）大きい | |
α＝0° β＝0° クーロンδ＝20° ランキンδ＝0°
| 項目 | クーロン | ランキン |
|---|---|---|
| 略図 |  |  |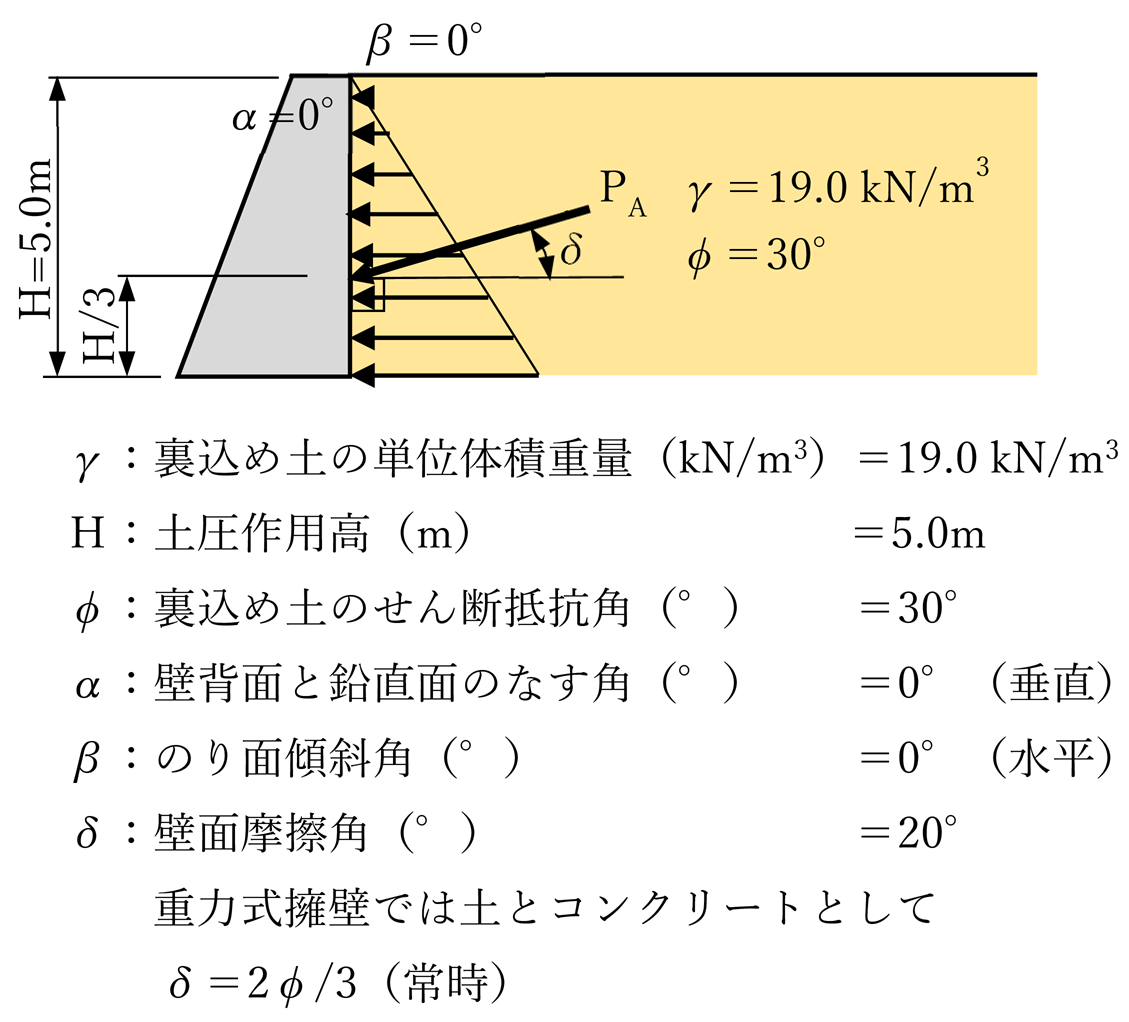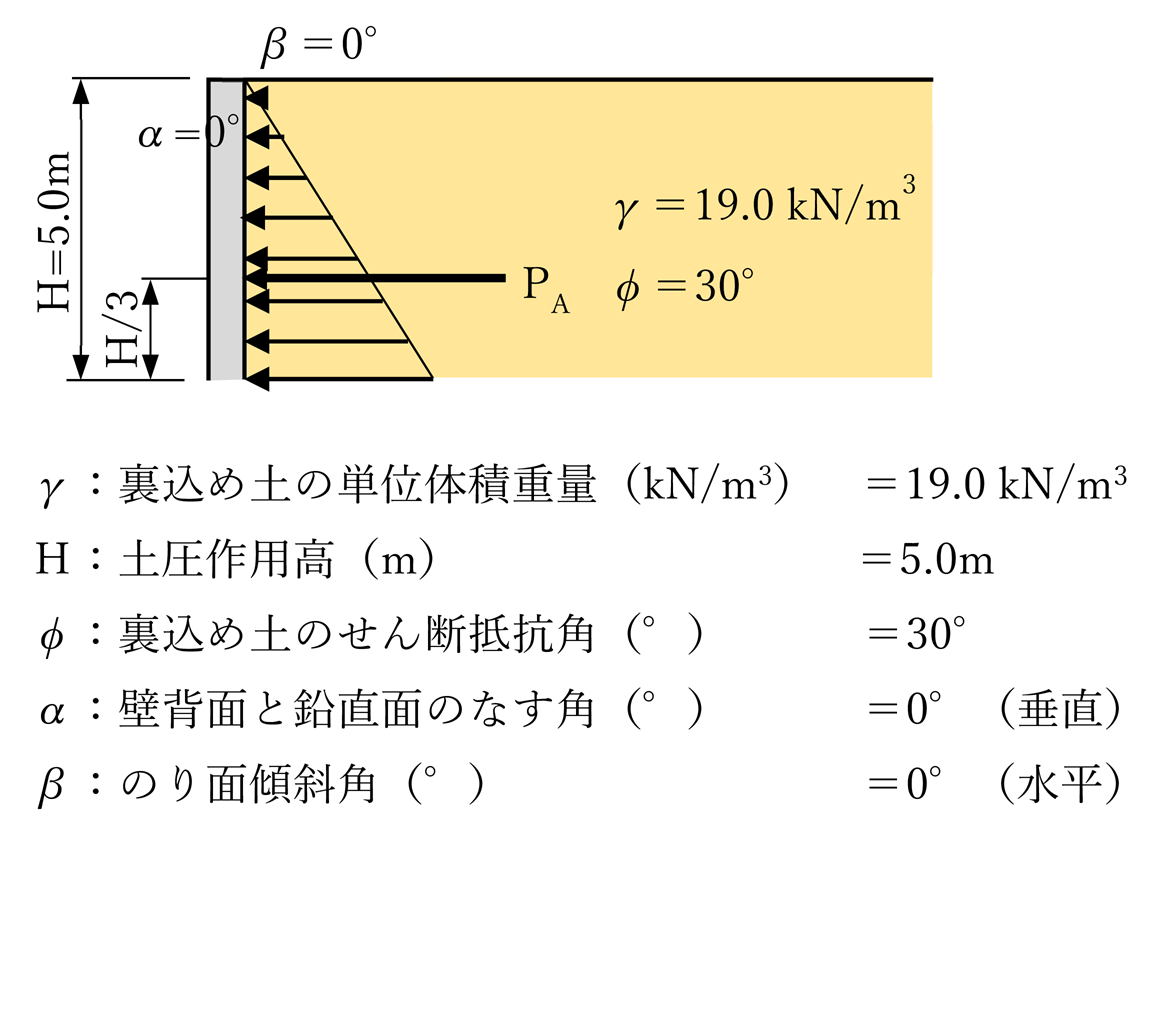
| 計算式 |  |  |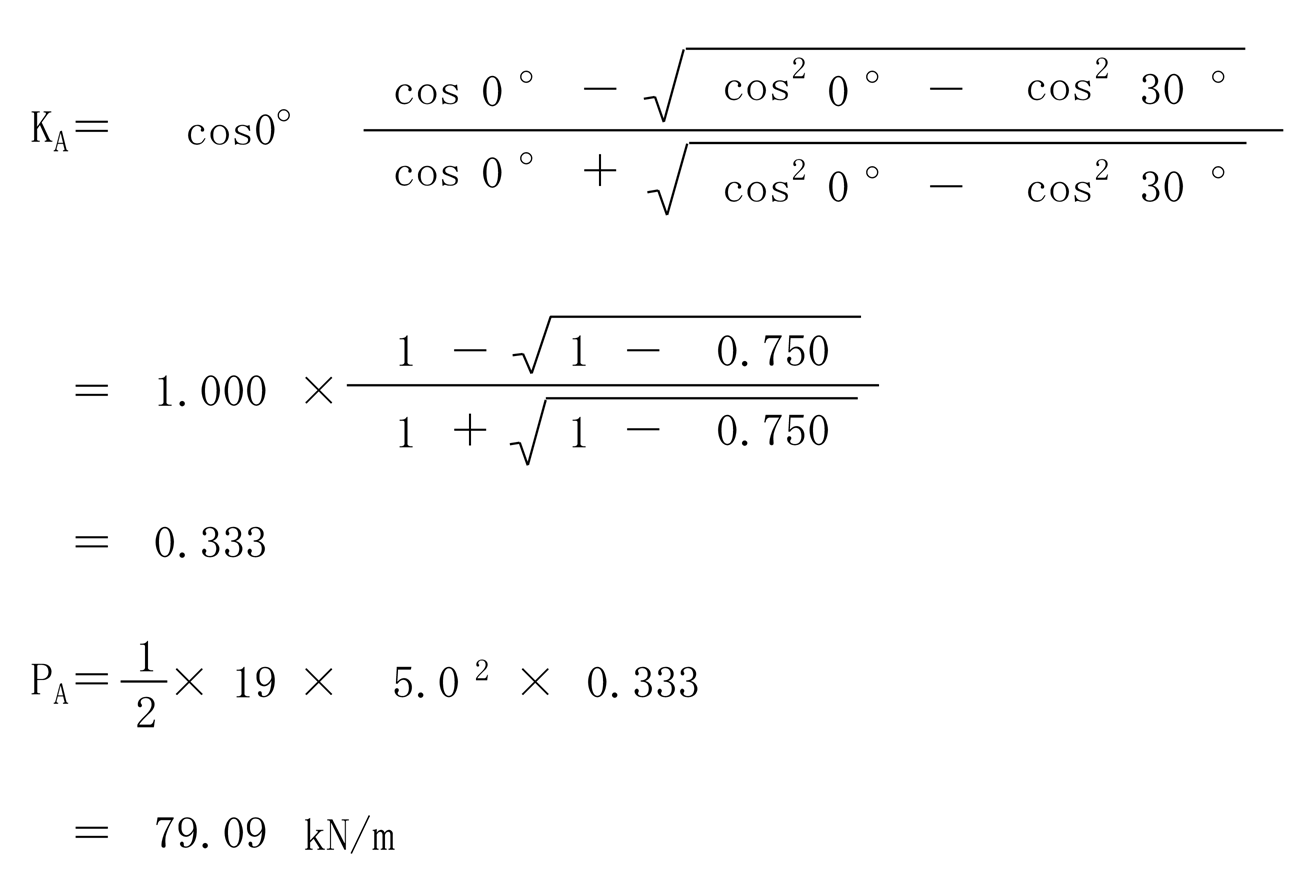
| 結果 | PA＝70.54kN/m | PA＝79.09kN/m |
| 評価 | ランキンの主動土圧が大きい（12.1％） | |
α＝0° β＝0° クーロンδ＝0° ランキンδ＝0° ※クーロンの前提条件はδ ≠ 0であるため参考計算
| 項目 | クーロン | ランキン |
|---|---|---|
| 略図 |  | |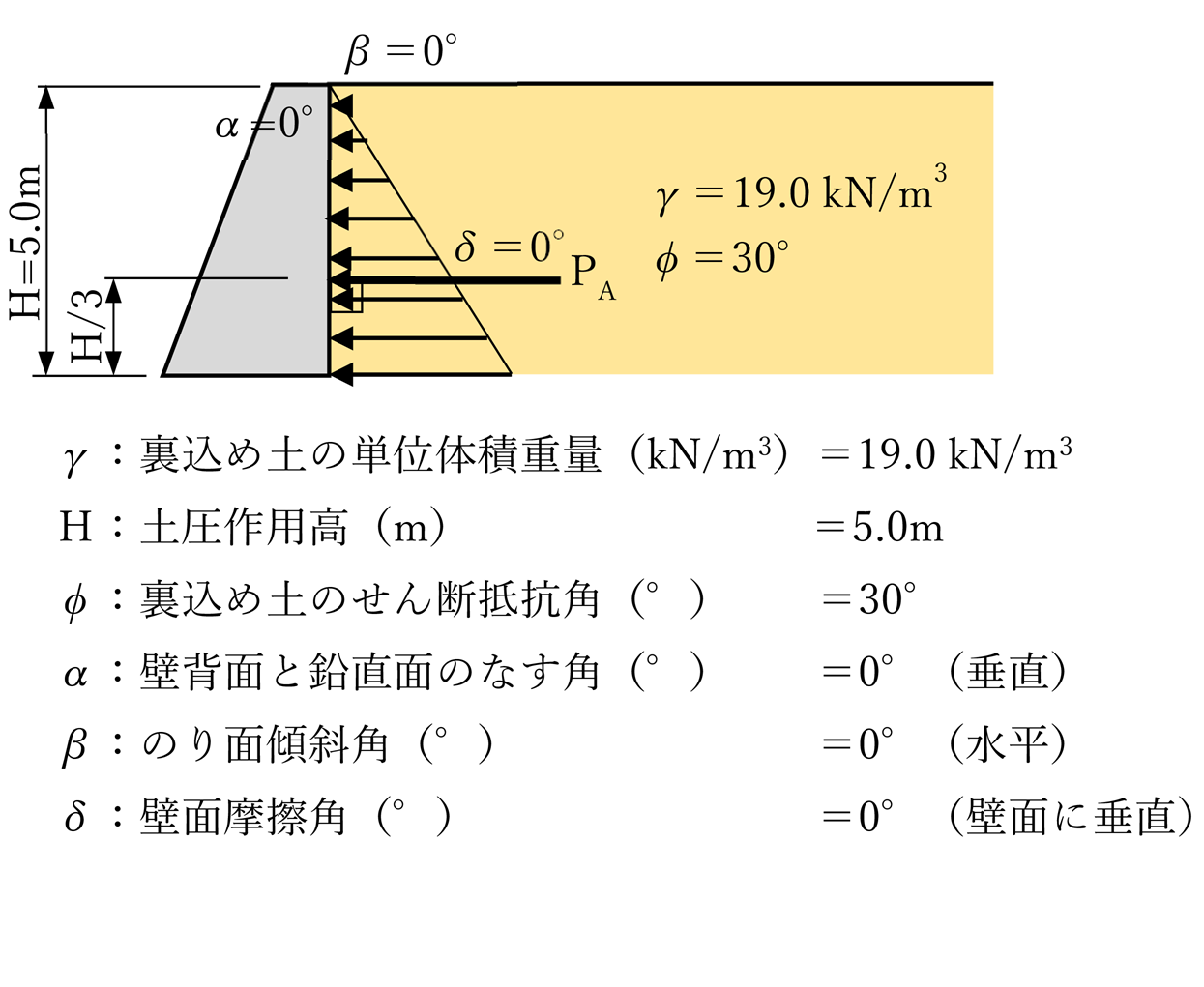
| 計算式 |  | |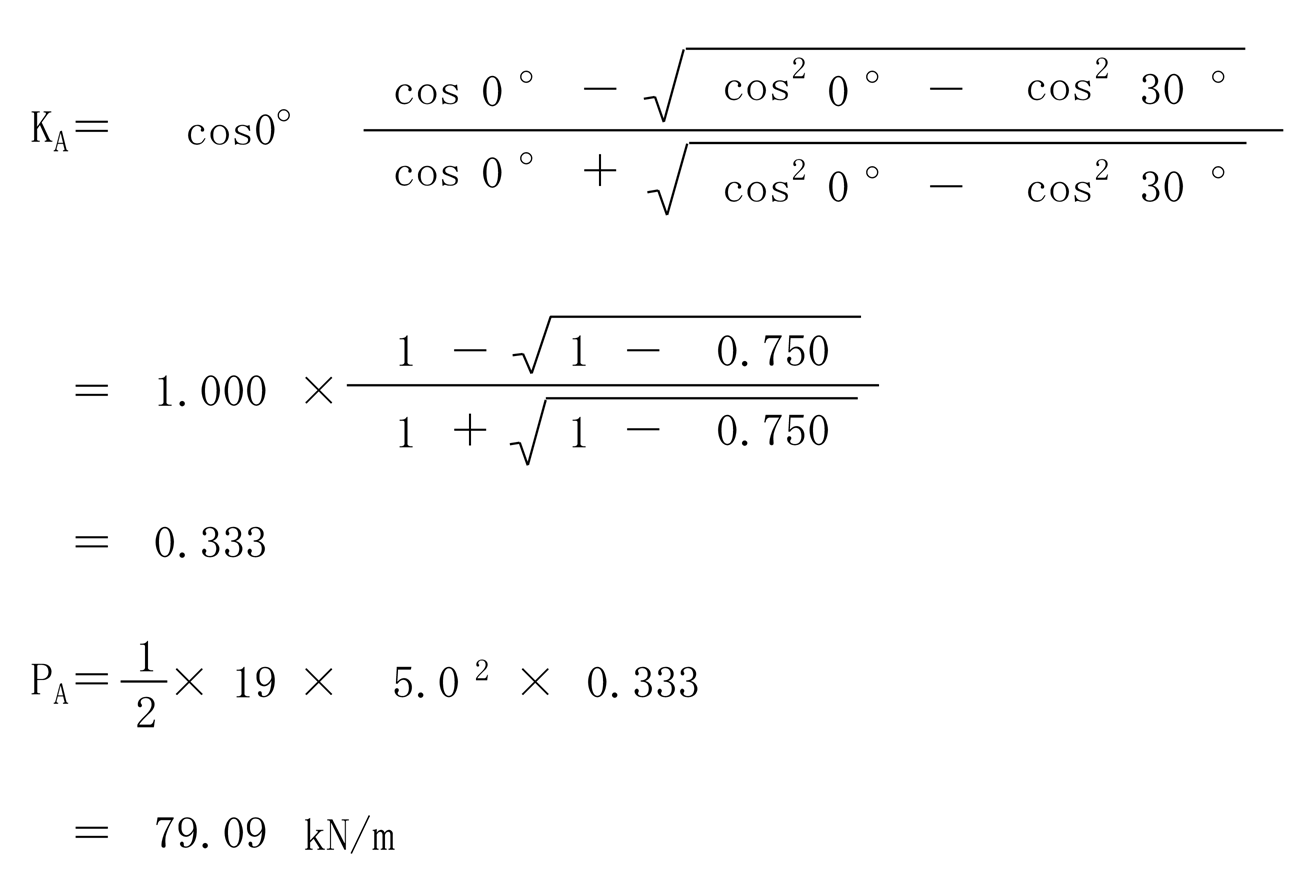
| 結果 | PA＝70.09kN/m | PA＝79.09kN/m |
| 評価 | 壁面摩擦角を考慮しなければクーロンもランキンも同じ | |
まとめ
クーロン土圧は壁面摩擦（δ=20°）を考慮し、土圧はδ傾き、滑り面は変動（例：ω≈55°）。ランキンは壁摩擦なし（δ=0°）、土圧は水平、滑り面は固定（θ=45°+ϕ/2=60°）。計算では、のり面あり（β=26.565°）でランキンの土圧が2.4%大きく、のり面なし（β=0°）で12.1%大きい結果に。クーロンのδ=0°（参考）では、両者とも同じ土圧（Pa≈79.09 kN/m）になりました。なぜか？ クーロンの壁摩擦は土圧を軽減し、δ=0°だとランキンと同じ条件になるためです。のり面（β）が大きいと摩擦の影響が減り、差が小さくなるのも確認できました。
